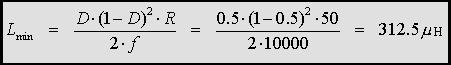4.7 Problemas resueltos
Problema nº1
Para el
chopper conmutado básico de la figura calcule
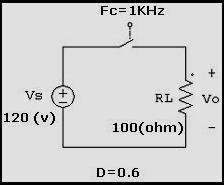
Figura 4.22
a)
Tensión media en
la carga
b)
Potencia media
absorbida
c)
Potencia media si
la frecuencia aumenta a 2 kHz
Solución
a)
![]()
![]()
b)
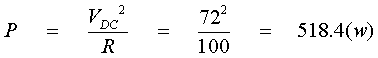
c) Al variar la frecuencia de conmutación no cambia la
tensión por lo que la potencia de salida se mantiene constante.
Problema
2
Para el chopper de la figura
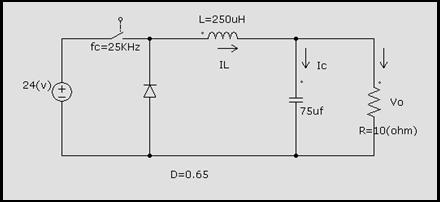
Figura 4.23
Calcular:
a) Vo, Imin, Imax y Rizado de Vo
Solución
a)
![]()
![]()
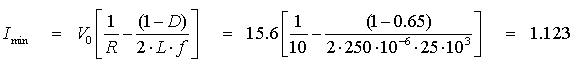
I mín = 1.123(A)
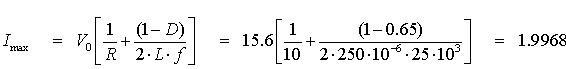
I máx = 1.9968(A)
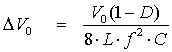
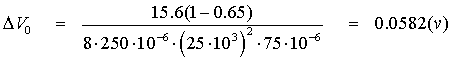
Problema 3
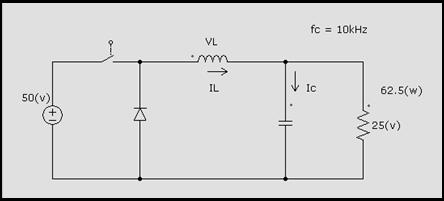
Figura 4.24
Para el sistema
de la figura determine:
a)
Ciclo de trabajo
b)
Valor de L que limite la corriente de pico a 6.25(A)
c)
Calcular C para limitar el rizado en la salida a un
0.5%
Solución
a)
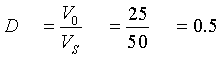
b)
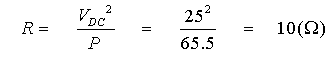
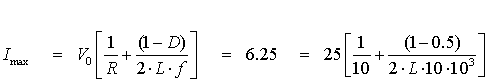
Despejando L
![]()
C)
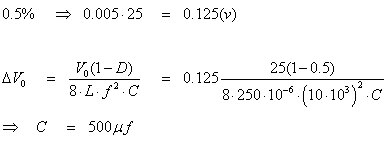
Problema 4
Diseñe un
convertidor reductor, la corriente en L debe ser permanente y el rizado < al
0.5%
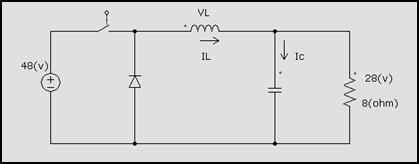
Figura 4.25
Solución:
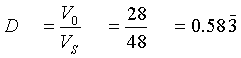
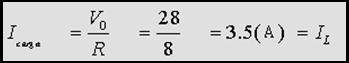
Para calcular la
inductancia mínima que asegura corriente permanente se iguala a cero la
expresión de Imín, y nos damos una frecuencia de conmutación de 10KHz.
![]()
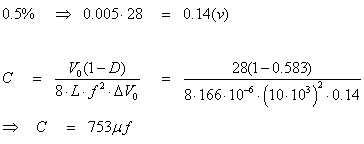
Problema 5
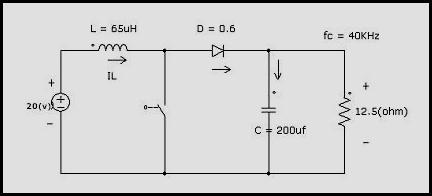
Figura 4.26
Para el convertidor de la
figura, se pide determinar:
a)
Tensión de salida
b)
Corriente media, máxima y mínima en L
c)
Rizado de la tensión de salida
Solución
a)
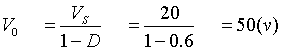
b)
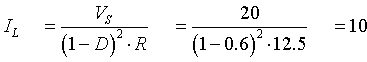
IL = 10(A)
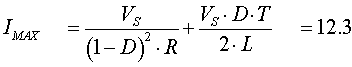
Imáx = 12.3(A)
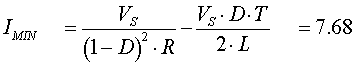
Imín = 7.68(A)
c)
![]()
Problema 6
Un chopper elevador presenta una
entrada de 5(v) una salida de 20(w) a 15(v), la corriente mínima en L no debe
ser menor que el 50% de la media, el rizado de la tensión de salida < 1% la
fc es 30 KHz. Determine el ciclo de trabajo, valor minimote L y valor mínimo de
C.
Solución:
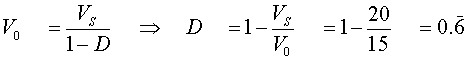
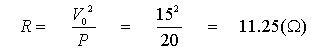
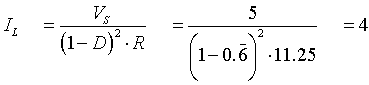
IL=4(A)
![]()
Imín = 2 (A)
Igualando la
expresión de Imin a 2 y despejando en función de L
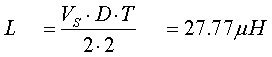
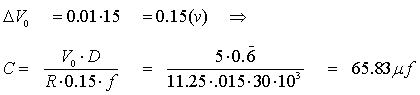
Problema 7
Diseñe
un convertidor elevador con una salida de 36(v) utilizando una entrada de
24(v), la carga es de 500(w) el rizado de la tensión de salida deberá ser menor
del 0.5% especifique el ciclo de trabajo, la frecuencia de conmutación, el
tamaño de la bobina y el condensador suponiendo corriente permanente.
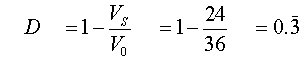
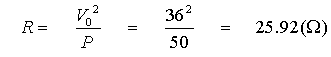
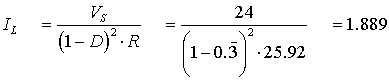
Con una frecuencia de conmutación de 40KHz
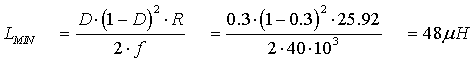
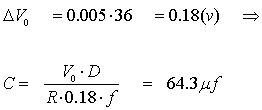
Problema 8
Para el convertidor de la figura se pide:
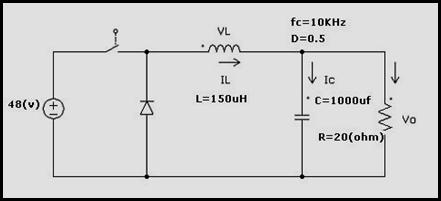
Figura 4.27
a)
Demuestre que IL es discontinua
b)
Tiempo durante el cual es discontinua
c)
Voltaje de salida
d)
Valor de resistencia para el cual se esta en el limite
de continuidad
Solución
a) Si la corriente es discontinua D1 debe ser menor que 1-D
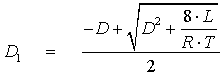
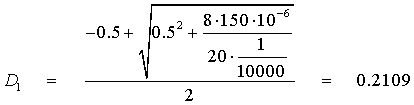
![]()
Corriente por la bobina
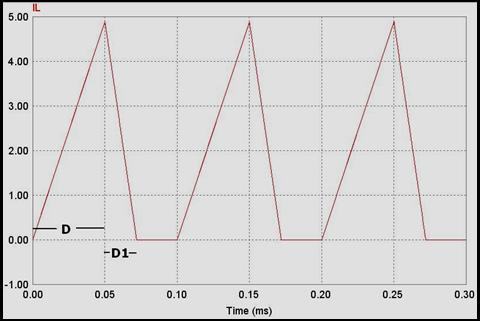
Figura 4.28
b)
El tiempo en
segundos de la discontinuidad es
![]()
c) Voltaje de salida
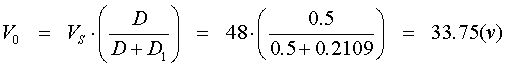
d) Para esto D1 = 1-D
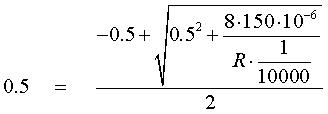
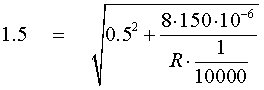
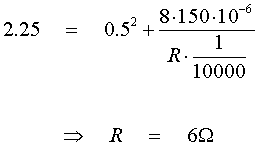
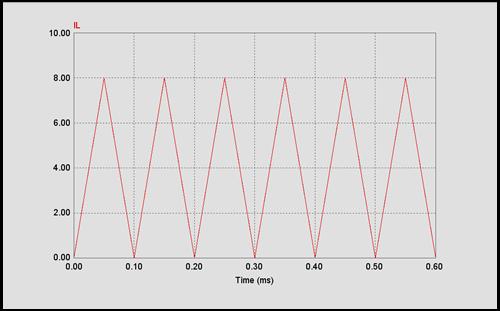
Figura 4.29
Problema 9
Para el convertidor elevador de la figura se pide:
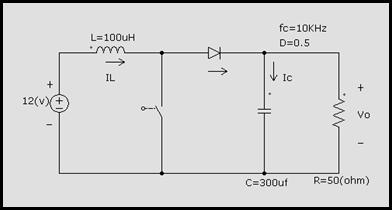
Figura 4.30
a)
Mostrar discontinuidad de IL
b)
Voltaje de salida
c)
Voltaje de salida si la corriente IL fuera permanente
d)
Valor de L que hace la corriente permanente
Solución
a)
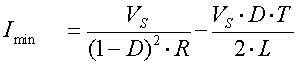
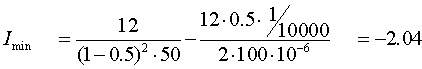
Imín = -2.04 (A)
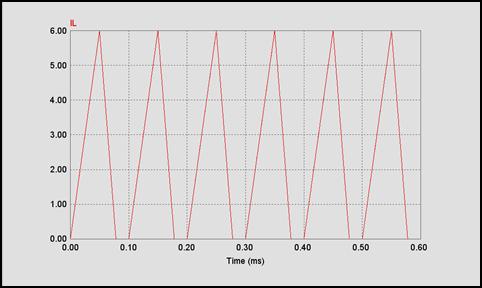
Figura 4.31
Como la corriente no puede ser negativa, se produce un
periodo de no-conducción
b)
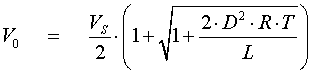
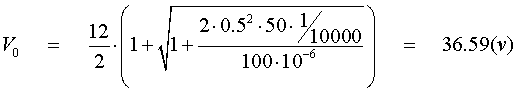
c)
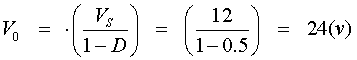
d)