|
|
circuito equivalente de la máquina |
Circuito equivalente del motor de inducción |
La diferencia entre la tensión aplicada a las fases del estator y la tensión inducida en éstas por el flujo resultante en el entrehierro, es igual a la suma de las caídas de tensión en la resistencia y en las reactancias de dispersión de los devanados del estator (situación idéntica a la del transformador).
|
|
circuito equivalente de la máquina |
Donde:
| R1 :Resistencia por fase del estator (W) R2 :Resistencia por fase del rotor, referido al estator (W) X1 :Reactancia de dispersión del bobinado de estator (W) X2 :Reactancia de dispersión del bobinado de rotor, referido al estator (W) Rc :Resistencia de pérdida en el núcleo (W) Xm :Reactancia de magnetización (W) S :Deslizamiento (%) Vf :Voltaje de fase (v) E1 :Voltaje inducido por fase (v) I1 :Corriente de estator (A) Mi :Corriente de magnetización (A) I2 :Corriente de rotor, referida al estator (A) |
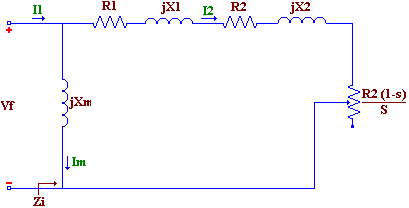
Cuando se necesita hacer resaltar las relaciones de torque y potencia, y a fin de simplificar los cálculos se propone el circuito equivalente simplificado. Como normalmente Rm es mucho más grande que Xm, y Xm >> (R1+X1), entonces Vf es aproximadamente igual a E1, luego el circuito simplificado es el siguiente:
 |
| Deslizamiento y Frecuencia Eléctrica en el Rotor |
Deslizamiento
Se le llama deslizamiento "S" a la diferencia entre la velocidad del campo magnético rotatorio y a la velocidad del rotor, es decir;
S = ns - nm (rpm)
donde:
| ns | = Velocidad del campo magnético rotatorio rpm |
| nm | = Velocidad del rotor rpm |
| S | = deslizamiento (%) |
A menudo se prefiere indicar el deslizamiento en porcentaje de la velocidad sincrónica:
S = ns - nm x 100 (%)
ns
Esta ecuación también puede expresarse en términos de velocidad angular (radianes por segundo) como:
S = ws - wm x 100 (%)
ws
Obsérvese que si el rotor gira a velocidad sincrónica , S=0, mientras que si el rotor está fijo, S=1. Todas las velocidades normales del motor, están en algún lugar entre estos dos límites.
Es posible expresar la velocidad mecánica del eje del rotor, en términos de velocidad sincrónica y de deslizamiento. Resolviendo las ecuaciones anteriores para velocidad mecánica resulta:
nm = ( 1 - S ) x ns o wm = ( 1- S ) x ws
Estas ecuaciones son útiles en la deducción del momento de torsión de los motores de inducción y de la relación de potencia.
Normalmente el valor de S, en estado estacionario, se encuentra entre un 4 y un 8%
Frecuencia eléctrica en el rotor
El motor de inducción trabaja induciendo voltajes y corrientes en el rotor de la máquina y por esa razón algunas veces se ha llamado Transformador giratorio. A la manera de un transformador, el primario (estator) induce un voltaje en el secundario (rotor) a través del flujo magnético, pero a diferencia del transformador, la frecuencia secundaria no es necesariamente la misma frecuencia primaria.
Si el rotor del motor es bloqueado, de forma tal que no se pueda mover, entonces el rotor y el estator de la máquina estarán a la misma frecuencia. Por el contrario, si el rotor gira a la velocidad sincrónica, la frecuencia del rotor será cero. En consecuencia para cualquier velocidad, la frecuencia del rotor será función directa del deslizamiento, y de la frecuencia eléctrica del estator. Lo anterior queda de manifiesto en la siguiente relación:
fr = S x fs (Hz)
donde:
| fr | = Frecuencia del rotor Hz |
| fs | = Frecuencia del estator Hz |
| S | = deslizamiento (%) |
| Potencia y torque desarrollado |
De la figura anterior se puede deducir:
La potencia desarrollada por el motor
![]()
La impedancia de entrada del motor
![]()
La corriente RMS del motor
![]()
Por otra parte, el torque en función de la potencia desarrollada por el motor, se obtiene de la siguiente expresión.
![]()
Donde:
Ws: es la velocidad sincrónica (rad/seg)
Por ultimo si consideramos el circuito equivalente propuesto en la figura 1.2, la expresión para el torque desarrollado por el motor queda como:
![]() (Ecuación 1.0)
(Ecuación 1.0)
| Característica de torque máximo y torque de arranque |
Torque máximo se obtiene cuando la potencia consumida por la resistencia R2/s sea máxima y un deslizamiento dado por S = Stmáx. Derivando la ecuación (1.0) respecto del deslizamiento, se obtiene:
![]()
si reemplazamos Stmáx en la ecuación (1.0), obtenemos el torque máximo desarrollado;
![]()
Para obtener el torque de arranque se sustituye la velocidad de la máquina igual a cero y el deslizamiento igual a uno, por lo que se obtiene:
![]()
| Funcionamiento
sin carga, a media carga y a carga máxima de un Motor Trifásico de Inducción |
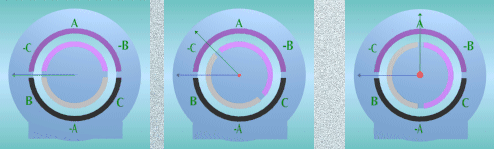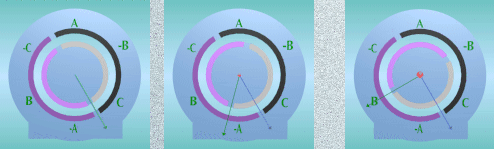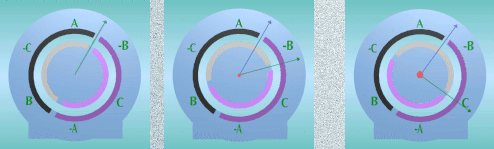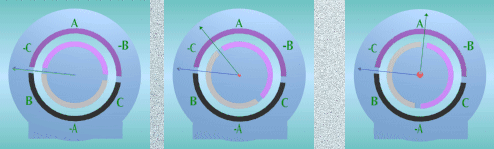 |
| Fig1 Fig 2 Fig 3 |
Fig1- Funcionamiento sin
Fig2-Funcionamiento a Fig3- Funcionamiento a
carga de un
media carga de un
carga máxima de un
motor de inducción
motor de inducción
motor
de inducción
donde: Fe = Fuerza Magnetomotriz del estator |
|
| Curva característica torque - velocidad del motor de inducción |
Si el motor está alimentado a partir de una tensión fija a una frecuencia constante, el torque desarrollado por el motor es una función del deslizamiento. En consecuencia la relación torque velocidad pueden determinarse a partir de la ecuación (1.0). Aquí se obtiene una curva como la que se muestra a continuación.
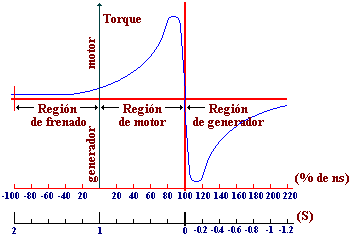 |
Existen tres regiones de operación:
Funcionamiento como motor, (0< S< 1):
El motor gira en la misma dirección que el campo. Una vez que el torque alcanza su nivel máximo, éste se reduce con el aumento del deslizamiento debido a una reducción del flujo en el entrehierro.
Regeneración, (S< 0):
La velocidad del rotor es mayor que la velocidad sincrónica en igual dirección y con un deslizamiento negativo. Por lo que la potencia es devuelta al circuito de estator y el circuito opera como generador.
Operación en sentido contrario, (S >1):
La velocidad del motor tiene sentido contrario a la dirección del campo, y el deslizamiento es mayor que la unidad.
Variaciones en las características de torsión-velocidad de un motor de inducción |
Característica T/S con resistencia adicional en el circuito del rotor |
Si la tensión de estator y la frecuencia de la red son constantes y con su valor nominal, al incorporar resistencia adicionales el circuito del rotor, las curvas características en función de la resistencia rotórica se muestra en la figura siguiente.
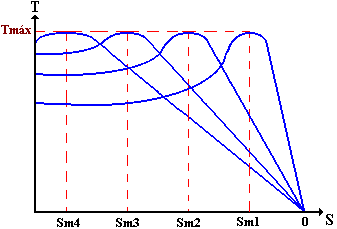 |
De la figura
podemos deducir:
a)El valor de torque máximo es independiente de la
resistencia rotórica.
b)El aumento de resistencias en el rotor implica un aumento
en el torque de partida y
deslizamiento al cuales se produce el
torque máximo.
| Característica T/S con tensión de alimentación variable |
Si la frecuencia de la red es constante y no existe resistencia adicional en el circuito del rotor al variar la tensión de estator se obtienen las curvas siguientes:
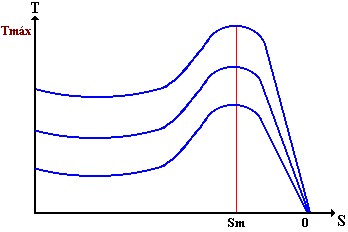 |
De la figura podemos deducir:
a)El valor del torque disminuye cuadráticamente con la disminución de la
tensión de
alimentación.
b)La variación de la tensión de
alimentación no afecta el valor del deslizamiento al cual se
produce el torque máximo.
| Característica T/S con frecuencia de alimentación variable |
La tensión inducida en el rotor se puede expresar:
![]()
Para operar la máquina a flujo constante, es decir, a torque constante se tiene:
![]()
Como no es posible actuar sobre la tensión “e”, si se desprecia la caída de tensión en el estator, se obtiene:
![]()
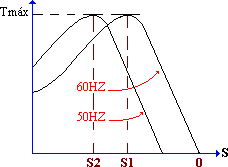
Por lo tanto, en el rango de frecuencia bajo la frecuencia nominal, se debe operar la máquina a torque constante.
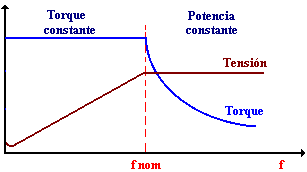
Ahora para operar la máquina a frecuencias mayores que la nominal, se mantiene la alimentación constante, lo cual implica operar en la zona de potencia constante con flujo en disminución. Esta situación implica que el torque en la máquina disminuye con el aumento de frecuencia manteniéndose constantes las pérdidas. En la siguiente figura se muestran las zonas de operación de la máquina operando con frecuencia variable.
 |