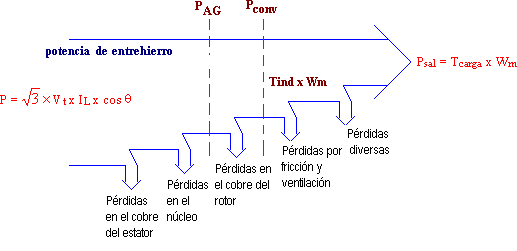
Pérdidas y diagrama de flujo de potencia |
Un motor de inducción se puede describir como un transformador giratorio trifásico, en el cual sus bobinados secundarios están cortocircuitados por lo que la potencia de salida no es eléctrica como en un transformador común, sino que es mecánica.
En la siguiente figura se ilustra la relación de la potencia de entrada (eléctrica) con la potencia de salida (mecánica).
 |
Diagrama de Potencia
Donde:
| Pent: | Es la potencia de entrada la cual se da en forma de corriente y voltaje trifásico. |
| Pscl: | Son las Pérdidas I²xR en los bobinados del estator. |
| Pnúcleo: | Son las Pérdidas por histéresis y por corrientes parásitas en el estator. |
| Prcl: | Son las Pérdidas I²xR en los bobinados del rotor. |
| Pf&w: | Son las Pérdidas por rozamiento y fricción a causa del movimiento del rotor. |
| Pmisc: | Son las Pérdidas diversas. |
| Psal: | Es la potencia de salida del motor, la cual es mecánica. |
| PAG: | Es la potencia que se traslada del estator al rotor por medio del entrehierro. |
| Pconv: | Es el punto de transformación de la potencia eléctrica en mecánica. |
| Potencia y momento de torsión en los motores de inducción |
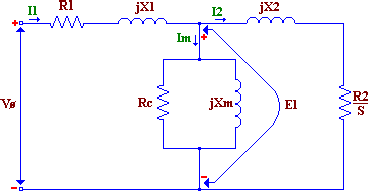 |
Del
circuito equivalente por fase de un motor de inducción se tiene:
Pérdidas del cobre del estator:
PCu_est = 3 x
I1 ² x R1
Pérdidas del núcleo en el estator:
Pnúcleo = 3
x E1 ² x Gc = 3 x (E1 ² / Rc)
La potencia del entrehierro se puede calcular por medio de:
Pentrehierro = Pent – PCu_est – Pnúcleo
Por lo tanto la potencia del entrehierro se puede encontrar por:
Pentrehierro = 3 x I´2 ² x (R´2 /s)
donde
R´2 = resistencia total del rotor, referida al estator
I´2 = Corriente del rotor, referida al estator
s = deslizamiento
Ahora, las pérdidas resistivas del rotor se obtienen aplicando la ecuación:
Protor = 3 x I´2 2 x R2
La potencia restante que cambia de eléctrica a mecánica es:
Pmecánica = Pentrehierro– Protor
Pmecánica = 3 x I²2 x R2 x (1/s –1 )
Por lo tanto se puede deducir:
| a) | Que mientras más bajo sea el deslizamiento del motor, la corriente rotórica disminuye y las pérdidas del rotor de la máquina son menores. |
| b) | Si el rotor no está girando el deslizamiento es igual a 1, y la potencia del entrehierro se disipa completamente en el cobre del rotor. |
| Momento inducido |
Se define como el momento generado por la conversión de potencia eléctrica en potencia mecánica interna, por lo que se puede obtener mediante la ecuación:
Tind = Pmecánica / Wrotor
También se puede obtener expresando la velocidad real en términos de la velocidad sincrónica, la cual es constante.
Tind = Pentrehierro / Wsincrónica