El autotransformador puede ser considerado simultáneamente como un caso particular del transformador o del bobinado con núcleo de hierro. Tiene un solo bobinado arrollado sobre el núcleo, pero dispone de cuatro bornes, dos para cada circuito, y por ello presenta puntos en común con el transformador . En realidad, lo que conviene es estudiarlo independientemente, pero utilizando las leyes que ya vimos para los otros dos casos, pues así se simplifica notablemente el proceso teórico.
En la práctica se emplean los autotransformadores en algunos casos en los que presenta ventajas económicas, sea por su menor costo o su mayor eficiencia. Pero esos casos están limitados a ciertos valores de la relación de transformación, como se verá en seguida. No obstante. es tan común que se presente el uso de relaciones de transformación próximas a la unidad, que corresponde dar a los autotransformadores la importancia que tienen, por haberla adquirido en la práctica de su gran difusión.
Para estudiar su funcionamiento, haremos como con los transformadores, es decir, primero consideraremos el principio en que se basan, desde el punto de vista electromagnético, para obtener las relaciones entre las tensiones y las corrientes de sus secciones, ya que no se puede hablar de bobinados en plural. Luego veremos el diagrama vectorial, muy parecido al de transformadores, pero con diferencias que lo distinguen netamente. Y, también, haremos un estudio comparativo entre el autotransformador y el transformador de iguales condiciones de servicio.
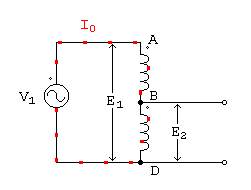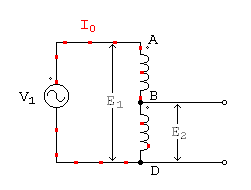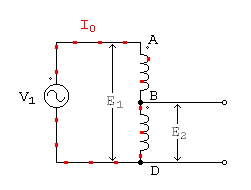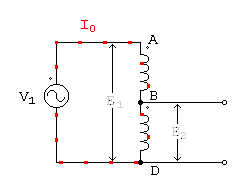
La figura siguiente nos muestra un esquema del autotransformador. Consta de un bobinado de extremos A y D, al cual se le ha hecho una derivación en el punto intermedio B. Por ahora llamaremos primario a la sección completa A D y secundario a la porción B D, pero en la práctica puede ser a la inversa, cuando se desea elevar la tensión primaria.

La tensión de la red primaria, a la cual se conectará el autotransformador, es V1, aplicada a los puntos A y D. Como toda bobina con núcleo de hierro, en cuanto se aplica esa tensión circula una corriente que hemos llamado de vacío en la teoría anterior. Sabemos también, que esa corriente de vacío está formada por dos componentes; una parte es la corriente magnetizante, que está atrasada 90° respecto de la tensión, y otra parte que está en fase, y es la que cubre las pérdidas en el hierro, cuyo monto se encuentra multiplicando esa parte de la corriente de vacío, por la tensión aplicada. Llamamos a la corriente total de vacío I0, como lo hemos hecho en otras oportunidades.
Ref: Francisco L. Singer, Transformadores Industriales, Neotécnica, Buenos Aires 1976.
Si se desprecia la no linealidad de las características de excitación, el autotransformador puede representarse por uno de los circuitos de la figura 1.

Figura 1: Circuitos equivalentes exactos de un autotransformador
Según el teorema de Thévenin, el autotransformador visto desde sus terminales de baja tensión equivale a una fuerza electromotriz igual a la tensión en circuito abierto Eocx medida entre los terminales de baja tensión, en serie con la impedancia Zscx medida entre los terminales de baja tensión con los terminales de alta en cortocircuito, como en la parte derecha del transformador ideal de la figura 1 (a). Si la razón de transformación del transformador ideal es VH / EocH, la tensión en sus terminales de alta es igual a la alta tensión VH del autotransformador real. Esta razón de tensiones en circuito abierto es muy aproximadamente igual a (N1 + N2) / N2 donde N1 y N2 son los números de espiras de los devanados serie y común, respectivamente. Puede demostrarse que si se conecta entre los terminales de alta del autotransformador ideal la admitancia en circuito abierto YocH medida desde el lado de alta tensión del transformador real, el circuito de la figura 1 (a) es un circuito equivalente exacto del autotransformador tanto para el lado de alta tensión como para el de baja. Evidentemente, si se realizan las medidas en circuito abierto en el lado de baja tensión y las medidas en cortocircuito desde el lado de alta tensión, también el circuito de la figura 1 (b) será un circuito equivalente exacto del autotransformador. Cuando se desprecia la corriente de excitación, los circuitos equivalentes exactos de la figura 1 se reducen a los circuitos equivalentes aproximados de la figura 2.
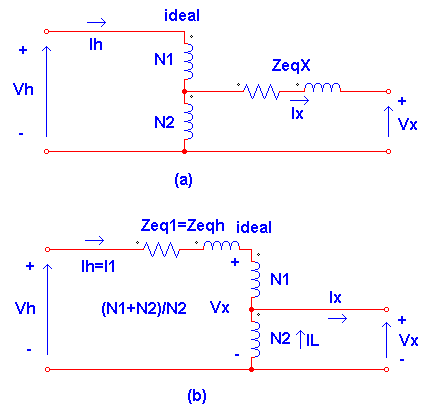
Figura 2: Circuitos equivalentes aproximados de un autotransformador
Los circuitos equivalentes son útiles para la determinación del comportamiento externo de los autotransformadores como elementos de circuito.
Interiormente, el autotransformador es exactamente igual que un transformador ordinario de dos circuitos, y por lo tanto, pueden deducirse circuitos equivalentes de la teoría de los transformadores de dos circuitos.
Ref: M.I.T., Circuitos Magnéticos y Transformadores, Reverté, Buenos Aires 1981.
Por otra parte, el rendimiento es más elevado cuando se realiza la conexión de autotransformador. Por ejemplo, si el rendimiento del transformador de 100 KVA a plena carga con factor de potencia unidad es 0.9825 cuando se conecta como transformador de dos circuitos, sus pérdidas son:
0.0175 x 100 / 0.9825 = 1.78 KW.
Cuando se conecta como autotransformador, sus pérdidas a plena carga siguen siendo 1.78 KW., pero estas pérdidas son ahora solamente
1.78 / 601.78 = 0.00296
de la potencia de entrada. En consecuencia, su rendimiento a plena carga con factor de potencia unidad como autotransformador es 0.99704. ¡casi perfecto!. En general el cociente entre en tanto por ciento o por uno de pérdidas de un transformador dado conectado como autotransformador y sus pérdidas como transformador ordinario de dos circuitos es el recíproco del cociente entre las potencias nominales para estas conexiones. Así, pues, por la ecuación:
Valor nominal como autotransformador / Valor nominal como transformador de dos circuitos = EH / (EH – EX)
Pérdidas a plena carga en % del valor nominal del autotransformador / Pérdidas a plena carga en % del valor nominal del transformador de dos circuitos = (EH – EX)/ EH
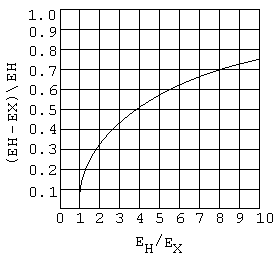
En la figura puede verse la variación de (EH – EX) / EH con el cociente EH / EX. Así, pues, cuando la razón de transformación EH / EX entre los circuitos de alta y baja tensión es inferior a 2:1, la variación unitaria de tensión (EH – EX) / EH que puede dar el transformador es menor que 1 / 2. Por lo tanto, el ahorro de tamaño y costo y el aumento del rendimiento cuando se utiliza un autotransformador en vez de un transformador de dos circuitos puede ser importante cuando EH / EX sea inferior a 2, si bien estas ventajas del autotransformador no son tan significativas para valores mayores de la razón de transformación EH / EX.
Ref: M.I.T., Circuitos Magnéticos y Transformadores, Reverté, Buenos Aires 1981.
ESTUDIO COMPARATIVO CON EL TRANSFORMADOR
Para hacer el estudio comparativo entre transformadores y autotransformadores, estableciendo las conveniencias del empleo de uno u otro, comenzaremos por considerar la prestación de un mismo servicio con dos unidades, una de cada tipo. La figura 1 nos da los dos esquemas que servirán par llegar a interesantes conclusiones.
Fig. 1. - Esquemas comparativos del autotransformador y el transformador.
En primer lugar, supondremos que las potencias aparentes en cada bobinado son proporcionales a las respectivas potencias efectivas, ya que los ángulos de fase entre carga y tensión dependen en su mayor grado de las condiciones que impone la impedancia Z conectada como carga. Escribamos, para el transformador, la siguiente igualdad:
V1 I1 = V2 I2
Que es válida si se desprecia la corriente de vacío, siempre pequeña, y las pérdidas, también muy pequeñas. La igualdad anterior dice que las potencias primaria y secundaria son iguales.
Restemos a ambos miembros una misma cantidad, con lo que la ecuación no se altera: esa cantidad es V2 I1, de significado únicamente algebraico:
V1 I1 – V2 I1 = V2 I2 – V2 I1
Pero ahora podemos agrupar términos de igual factor, con lo que se tiene:
I1 (V1 - V2) = V2 (I2 - I1)
Y analizando esta expresión, diremos: el primer miembro se hace nulo cuando el punto B coincide con el A; además, está dado por el producto de la tensión entre A y B, primario ficticio, por la corriente que circula entre esos puntos, o sea es la potencia que el primario transfiere por vía electromagnética al secundario. El segundo miembro está dado por el producto de la corriente que circula en la sección secundaria, por la tensión entre los extremos de esa sección, luego, es la potencia que recibe el secundario por vía electromagnética,. transferida desde el primario, según ya sabemos. Si no hay pérdidas, las dos potencias resultantes son iguales. El resto de la potencia que recibe el secundario, hasta llegar a la cifra dada por el producto V2 I1, llega a él por vía directa. sin que intervenga el primario, o sea que llega lo mismo con autotransformador o sin él.
Volvamos a las dos ecuaciones que dan la igualdad de potencias aparentes. La segunda corresponde al autotransformador, y tomando sólo el primer miembro, se puede escribir, llamándolo Pa, potencia del autotransforrnador:
Pa = I1 (V1-V2) =I1 V1 (1 – V2/V1) = I1 V1 (1- 1/k)
Pa = I1 V1 (k-1)/k
Donde en todo el proceso no se ha hecho otra cosa que artificios algebraicos, a fin de que aparezca la relación de transformación k, como cociente de la tensión primaria y secundaria. Ahora tomemos la potencia aparente del transformador, que llamaremos Pt, necesaria para rendir el mismo servicio; ya la tenemos expresada en la igualdad que teníamos al principio de este estudio, de la cual sólo tomamos el primer miembro:
Pt = V1 I1
Pues con esta potencia suministramos al secundario una corriente de carga I2 bajo una tensión V2, es decir, lo mismo que nos rinde el autotransformador. Si se divide la expresión que da la potencia necesaria del autotransformador por la del transformador, se llega a la relación:
(Pa / Pt) = (k - 1) / k
Que nos dice que, un autotransformador que nos presta igual servicio que un transformador, tiene menor potencia, luego podrá ser más pequeño, liviano y barato. La relación entre ambas potencias es pequeña para valores de k grandes. Es decir que, por lo que atañe a la potencia en juego en el autotransformador, conviene utilizarlo para relaciones de transformación del orden de la unidad. Para relaciones muy diferentes, las tensiones en los bobinados primario y secundario son muy distintas y se crean problemas de aislación que pueden decidir la no conveniencia del autotransformador.
Además de la menor potencia necesaria, tenemos que serán menores las pérdidas en el cobre, por circular en la sección secundaria del bobinado una corriente reducida.
Como en las consideraciones anteriores siempre hemos supuesto mayor a la tensión primaria, y puede no serlo, veamos lo que sucede en tal caso. La figura 2 da el esquema para el caso que se desee tener una tensión secundaria mayor que la de la red. La derivación en el bobinado permite conectar la red, y la carga se conecta entre extremos del bobinado.
En la deducción anterior que estudiaba la energía puesta en juego, se supuso que las pérdidas eran nulas, de modo que la potencia primaria era igual a la secundaria. Luego, podemos considerar como primarios a cualquiera de las dos secciones; de esto se desprende que serán válidas las consideraciones hechas para el esquema de la figura 1 en el caso del de la figura 2.
Luego, convendrá el empleo del autotransformador en todos los casos que no se creen problemas de aislación entre el circuito primario y secundario, pues la potencia necesaria es menor. Para valores de k cercanos a la unidad, y en este caso (fig. 2) serán fraccionarios por ser la tensión primaria menor, la potencia necesaria será muy pequeña, y nunca convendrá utilizar un transformador, salvo que se desee aislar el circuito secundario de la red primaria.
Fig. 2. - Autotransformador elevador de tensión.
Veamos, por ejemplo, un caso práctico. La red tiene tensiones que oscilan entre 200 y 250 Volt, y se desea intercalar un autotransformador con varias derivaciones, a fin de tener siempre una tensión secundaria de 220 Volt.
La relación de transformación necesaria oscila entre:
k = 200 / 220 = 0.91 ; y k = 250/220 = 1.14
Con lo que la potencia necesaria del autotransformador será, con respecto a la de un transformador que prestara igual servicio:
(0.91 – 1) / 0.91 = 0.1 = 10 %
Donde se toma el valor absoluto del cociente, prescindiendo del signo, por razones obvias. Para el otro límite extremo de tensiones, el cociente vale:
(1.14 – 1) / 1.14 = 0.12 = 12 %
Luego, la potencia necesaria del autotransformador es sólo un 12 % (tomando la relación más desfavorable, pues esa será la cifra necesaria) de la que debería traer un transformador que prestará el mismo servicio. Estas cifras son elocuentes de por sí, y bastan para demostrar la razón del empleo generalizado de los autotransformadores en las redes, para elevar o reducir la tensión en valores cercanos a la unidad.
Para relaciones de transformación que se alejan mucho de la unidad, el cociente entre las potencias necesarias tiende a valer 1, luego al autotransformador requiere casi la misma potencia que el transformador. Pese a esto sería conveniente por sus menores pérdidas y caídas internas, pero .en tales casos hay mucha diferencia entre las tensiones primaria y secundaria, con lo qué aparecen problemas de aislación; ellos obligan a utilizar el transformador, cuya independencia entre circuito primario y secundario le da ventaja en tales casos.
Ref: Francisco L. Singer, Transformadores Industriales, Neotécnica, Buenos Aires 1976.
La corriente de excitación tiene menos importancia cuando el transformador funciona como autotransformador que cuando lo hace como transformador de dos circuitos. Si las tensiones de los devanados tienen sus valores nominales a carga nula, el flujo en el núcleo tiene su valor nominal y los ampere – espira totales en vacío son los mismos tanto si el transformador está conectado como autotransformador como si lo está como transformador ordinario de dos circuitos. La corriente de excitación varía inversamente con el número de espiras por las que circula la corriente de excitación. Como las tensiones nominales son proporcionales a los números de espiras, los volt – ampere de excitación a la tensión normal son los mismos tanto si el transformador está conectado como autotransformador como si lo está como transformador ordinario de dos circuitos.
Ij en % como autotransformador / Ij en % como transformador de dos circuitos
= (EH – EX) / EH
Esta relación es aplicable a un transformador dado conectado como autotransformador o como transformador de dos circuitos. Es sólo aproximadamente la razón de la corriente de excitación de un autotransformador a la de un transformador de dos circuitos diferentes, pero de igual valor nominal, ya que el porcentaje de la corriente de excitación en los diseños normales varía algo como el tamaño.
El despreciar la corriente de excitación en un transformador ordinario de dos circuitos suele introducir un error pequeño, excepto en el análisis de problemas relacionados directamente con los fenómenos de excitación, especialmente de aquellos en los que interviene el comportamiento de los armónicos. Como, por lo general, la corriente de excitación de un autotransformador es muy débil, el despreciarla introduce un error aún menor.
Si los volt – ampere de excitación del transformador de 100 KVA de la figura funcionando como transformador de dos circuitos son el 3 %, o sea 3 KVA sus volt – ampere de excitación conectado como autotransformador siguen siendo 3 KVA. No obstante, esto no es más que el 0.5 % de su potencia nominal de 600 KVA que tiene funcionando como autotransformador.

Ref: M.I.T., Circuitos Magnéticos y Transformadores, Reverté, Buenos Aires 1981.
Si se conecta una impedancia Z entre los puntos B y D, tal como lo muestra la figura 58, sin entrar en consideraciones sobre el carácter de Z, por ahora, se producirá una variación en las condiciones de funcionamiento. Z puede tener carácter óhmico, inductivo o capacitivo. Al conectarla entre dos puntos que acusan una diferencia de potencial, circulará una corriente, que llamamos I2, con subíndice correspondiente a secundario, pues así lo hemos especificado al principio.
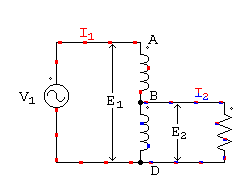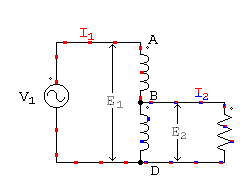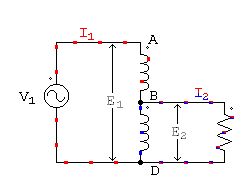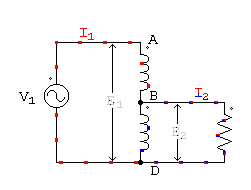
Autotransformador reductor
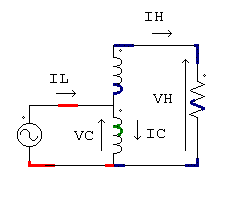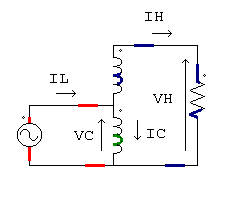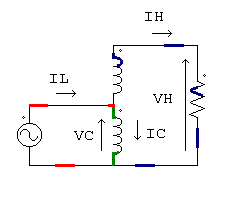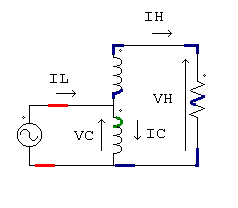
Autotransformador elevador
Para determinar el sentido instantáneo de esta corriente secundaria hagamos la siguiente observación: en un dado instante, la f.e.m. inducida es tal que el punto A tiene mayor potencial que el D. Luego los vectores de las ff.ee.mm. E1 y E2 podemos imaginarlos dibujados con la flecha hacia arriba. La tensión primaria debe vencer a la f.e.m. primaria, luego en ese instante la corriente primaria circula con sentido contrario al que correspondería a la f.e.m. primaria, es decir, de A hacia D. En el secundario, en cambio, la tensión en los bornes y la f.e.m. tienen el mismo sentido, luego la corriente circula hacia arriba, es decir, de D hacia B.
¿Qué sucede en el tramo B D donde tenemos dos corrientes encontradas?
Que sólo circulará la diferencia entre ambas, es decir, que en el tramo secundario del bobinado circula una corriente:
IBD = I2 – I1
Debiendo aclararse que esta diferencia debe tener carácter vectorial. Pero ya se comienza a palpar una de las ventajas del autotransformador. En una sección del bobinado circula sólo la diferencia de las corrientes primaria y secundaria. Quiere decir que en el tramo A B tenemos la corriente I1; en el BD tenemos la diferencia (I2 -I1) y, en el circuito de carga tenemos la corriente I2. En estas consideraciones estamos prescindiendo de la corriente de vacío, porque ya sabemos que es de valor muy pequeño comparada con la primaria de carga. Procediendo así se pueden hacer simplificaciones importantes.
Veamos la relación entre las corrientes primaria y secundaria. Haciendo abstracción de la corriente magnetizante, por su pequeñez, sabemos por lo que se estudió en el primer capítulo, que los ampervueltas primarios deben ser iguales a los ampervueltas secundarios, luego podemos escribir en este caso, y aclarando que la expresión es algebraica y no vectorial, por lo que estudiamos para transformadores al despreciar I0:
N1 I1 = N2 I2
Que por simple cambio de miembro de sus factores permite escribir:
(N1 / N2 ) / (I2 / I1) = k
Relación que es inversa a la de tensiones o ff.ee.mm., lo mismo que sucedía para los transformadores. Si queremos conocer la relación entre las corrientes circulantes en la sección superior e inferior del bobinado, podemos proceder así: En primer lugar, sabemos ya que:
IBD = I2 – I1
Y si dividimos esta ecuación por la corriente primaria, o sea por la corriente que circula entre A y B, se tiene:
(IBD / IAB) = (I2 / IAB) – (I1 / IAB)
Ahora analicemos lo que ha resultado; el primer término es el cociente entre las corrientes que queríamos obtener; el segundo término es la relación de transformación., pues el denominador es la corriente I1, y el tercer término es la unidad, por ser iguales el numerador y denominador. Luego, se tiene:
(IBD / IAB) = k - 1
relación cuyo primer miembro es inverso al similar que se obtuvo para las tensiones, pues el segundo miembro de ésta es igual al de la expresión que daba la relación entre las ff.ee.mm. de las secciones superior e inferior.
Si se consideran aisladamente las dos expresiones que han dado por resultado (k - 1), que son los cociente entre las ff.ee:mm. entre puntos A B y B D, y las corrientes circulantes entre B D y A B,
podemos suponer al autotransformador como equivalente de un transformador que en lugar de k, tenga una relación de transformación (k – 1), y cuyo primario sea la sección superior A B y cuyo secundario sea la sección B D. Esto es importante en lo que respecta a la transferencia de energía desde la red al circuito de carga en el secundario, pues en ese aspecto, parte de la energía se transfiere por vía electromagnética, como en los transformadores, y parte por vía eléctrica directa, como en un circuito cerrado simple de corriente alternada. La parte que transfiere energía por vía electromagnética es la A B. que obra como primario ficticio, y la parte que la recibe transferida es la B D, secundario ficticio. Cuando comparemos las características del autotransformador con el transformador volveremos sobre este detalle, para demostrarlo, y para poner de manifiesto una de las cualidades fundamentales del primero, que le da ventajas evidentes con respecto al segundo.
Ref: Francisco L. Singer, Transformadores Industriales, Neotécnica, Buenos Aires 1976.
1.-Conexión en estrella de autotransformadores.
Tres autotransformadores monofásicos pueden conectarse en estrella, como se indica en la figura (A).En estas condiciones, el comportamiento del banco es análogo, en muchos aspectos, al de un banco de tres transformadores de dos circuitos conectados en estrella – estrella. Si el neutro está aislado, como el de la figura (A), las tensiones respecto al neutro están desequilibradas a menos que los transformadores tengan características de excitación exactamente iguales. Además, las tensiones entre línea y neutro contienen terceros armónicos relativamente grandes originados por la supresión de los terceros armónicos de las corrientes de excitación.

2.-Conexión en triángulo de autotransformadores.
Tres autotransformadores pueden conectarse en triángulo en la forma indicada en la figura (B). Un posible inconveniente de esta conexión es que las tensiones de línea de los secundarios no están en concordancia de fase con las tensiones de línea de los primarios. Además, la mayor razón de transformación que puede obtenerse es 2 : 1 . Como en la conexión triángulo – triángulo de transformadores de dos circuitos, los terceros armónicos de las corrientes de excitación circulan por el triángulo, pero no aparecen en las corrientes de línea.
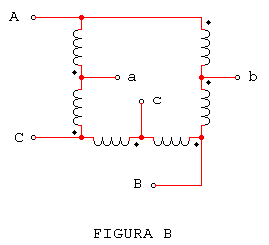
Los autotransformadores también pueden conectarse en triángulo como se indica en la figura (C). En la cual los devanados serie se conectan en serie con las líneas de alta tensión y los devanados comunes se conectan en triángulo. Al igual que la conexión triángulo de la figura (B), las tensiones de línea del primario y secundario no están en fase.
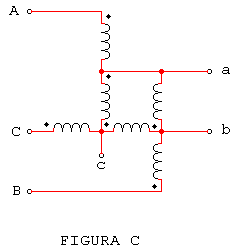
3.-Conexión de autotransformadores en triángulo abierto.
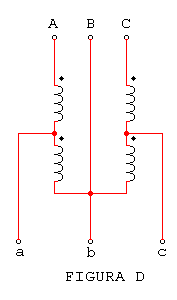
A diferencia de la conexión en triángulo, la conexión en triángulo abierto de autotransformadores, indicada en la figura (D), no está restringida a razones de transformación inferiores a la 2 : 1. Además, si se prescinde de las caídas de tensión debidas a las impedancias de fuga, las tensiones de línea del primario y secundario están en concordia de fase.
Luego, si se conectan ambos lados del primario y secundario de un banco de autotransformadores conectados en triángulo abierto a circuitos conectados en estrella, sólo podrá conectarse a tierra el neutro de uno de los lados del banco, ya que existe una diferencia de tensión entre los neutros de los circuitos primarios y secundarios.
Ref: M.I.T., Circuitos Magnéticos y Transformadores, Reverté, Buenos Aires 1981.