 |
Los transformadores para circuitos trifásicos pueden construirse de dos maneras. Estas son:
|
Casi todos los sistemas importantes de generación y distribución de potencia del mundo son, hoy en día, sistemas de ca trifásicos. Puesto que los sistemas trifásicos desempeñan un papel tan importante en la vida moderna, es necesario entender la forma como los transformadores se utilizan en ella.
 |
Los transformadores para circuitos trifásicos pueden construirse de dos maneras. Estas son:
|
Para el análisis de su circuito equivalente, conviene representar cada uno de los transformadores monofásicos que componen un banco trifásico por un circuito equivalente. Como los efectos de las capacidades de los devanados y de los armónicos de las corrientes de excitación suelen ser despreciables, podrá utilizarse cualquiera de los circuitos equivalentes deducidos para el caso de los monofásicos; los más útiles para el presente estudio son los de la figura 1.
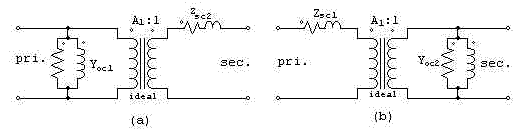
En ellos, el transformador esta representado, como en el teorema de Thévenin, por su impedancia en cortocircuito en serie con su tensión en circuito abierto; la razón de las tensiones en circuito abierto está representada por un transformador ideal; y las características de excitación están representadas por la admitancia en circuito abierto.
Los valores de los parámetros pueden obtenerse a partir de los datos de diseño o ensayos en circuito abierto o en cortocircuito tomados a uno u otro lado del transformador, y estos valores se pueden emplear, sin modificación, o en el circuito equivalente de la figura 1a (en el cual se coloca la admitancia de excitación en el lado primario) o en el circuito equivalente de la figura 1b (en el cual se coloca la admitancia de excitación en el lado del secundario) En muchos problemas, los efectos de la corriente de excitación son tan pequeños que puede despreciarse por completo la corriente de excitación y representarse el transformador por su impedancia equivalente en serie con un transformador ideal. Si se quiere, las impedancias equivalentes y admitancias de excitación de la figura 1 se puede referir al otro lado del transformador multiplicando o dividiendo, según sea el caso, por el cuadrado de la razón de transformación.
El circuito equivalente de un banco trifásico de transformadores puede trazarse conectando los circuitos equivalentes de las unidades de acuerdo con las conexiones del banco. Por ejemplo, en la figura 2a puede verse el circuito equivalente de un banco estrella-estrella y en la figura 2b un circuito equivalente de un banco triángulo. En la figura 2, las Y representan las admitancias en circuito abierto o de excitación y las Z las impedancias en cortocircuitos o equivalentes.
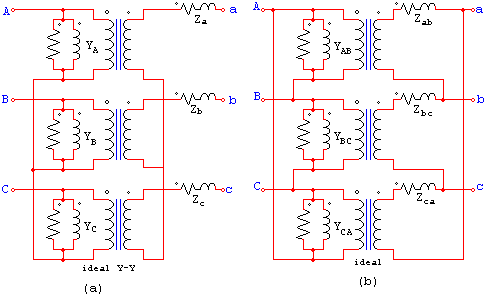
En el análisis de sistemas de potencia es frecuentemente necesario combinar las impedancias de los transformadores con las impedancias de las líneas de transmisión a las que están conectados. Luego, resulta a menudo conveniente representar un grupo de devanados conectados en triángulo por un circuito equivalente conectado en estrella, ya que en la conexión en estrella las impedancias equivalentes que representan a los transformadores están en serie con los tres terminales de línea y por lo tanto pueden sumarse directamente a las impedancias de fase de los circuitos de transmisión. Ya se sabe que, visto desde sus tres terminales, un triángulo de elementos de circuito puede sustituirse por una estrella equivalente. Así, las admitancias de excitación YAB , YBC , YCA conectadas en triángulo de la figura 2b son equivalentes a las admitancias YA , YB , YC conectadas en estrella cuyos valores vienen dados por las conocidas relaciones.
YA = (YAB YBC + YBC YCA + YBC YCA ) / YBC
YB = (YAB YBC + YBC YCA + YBC YCA ) / YCA
YC = (YAB YBC + YBC YCA + YBC YCA ) / YAB
Además, las impedancias Zab , Zbc , Zca de la figura 2b que forman parte de un sistema conectado en triángulo, pueden sustituirse por impedancias conectadas en estrella. Así, el teorema de Thévenin, el banco triángulo-triángulo de la figura 2b es equivalente en su lado de secundarios a un generador conectado en estrella que cree las mismas tensiones de secundario entre línea y línea en circuito abierto y conectado en serie con impedancias cuyos valores sean las equivalentes en estrella de las impedancias en cortocircuito de los transformadores medidas desde los terminales de sus secundarios. Luego, los transformadores ideales conectados en triángulo-triángulo de la figura 2b pueden sustituirse por un banco estrella-estrella que dé las mismas tensiones en circuito abierto, y las impedancias en cortocircuito de los transformadores pueden representarse por impedancias en estrella conectadas en serie con cada terminal de línea. Las relaciones entre las impedancias en cortocircuito Za , Zb , Zc vienen dadas por las conocidas relaciones,
Za = (Zab Zca) / (Zab + Zbc + Zca)
Zb = (Zab Zbc) / (Zab + Zbc + Zca)
Zc = (Zbc Zca) / (Zab + Zbc + Zca)
Por tanto, por lo que concierne a sus efectos sobre los circuitos exteriores, un grupo de devanados conectados en triángulo puede representarse por un circuito equivalente conectado en estrella, como en la figura 2a, con tal que los parámetros de la estrella equivalente estén relacionados con los parámetros reales de los transformadores conectados en triángulo en la forma indicada por las ecuaciones anteriores y con tal que las tensiones en circuito abierto entre línea y línea del circuito equivalente conectado en estrella sean las mismas que las de los devanados conectados en triángulo. Es decir, en el caso de un banco triángulo-triángulo los transformadores ideales pueden sustituirse por un banco estrella-estrella que dé las mismas tensiones de funcionamiento. Análogamente, a menudo se representa un banco triángulo-estrella (o estrella-triánfgulo) por un circuito equivalente estrella-estrella, como en la figura 2a, que dé las mismas magnitudes de las tensiones en circuito abierto entre línea y línea. Sin embargo, a causa del desfasaje introducido por la conexión triángulo-estrella, el circuito equivalente estrella-estrella de un banco triángulo-estrella no presenta las relaciones correctas de fase entre las corrientes de primario y secundario o entre las tensiones de primario y secundario, aun cuando presente correctamente las relaciones entre las corrientes y tensiones de cada lado.
Ref: M.I.T., Circuitos Magnéticos y Transformadores, Reverté, Buenos Aires 1981.
Para obtener los diagramas vectoriales de un transformador trifásico tipo núcleo o asimétrico, hay que estudiar en forma detallada lo que sucede en un nuclelo tipo nucleo de tres ramas como el que se muestra en la siguiente figura 3.
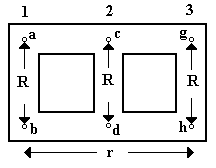
Figura 3. Nucleo trifasico tipo nucleo de tres ramas
De la figura consideramos a las partes del núcleo comprendidas entre los puntos a-b, c-d y g-h como ramas pertenecientes a cada fase, o ramas del núcleo. Las zonas comprendidas entre a y g y entre b y h son las culatas, e influirán en forma distinta para cada rama. La reluctancia magnética de cada rama la indicamos con R, y suponemos qué son las tres iguales, lo que es cierto; la reluctancia de cada culata la llamarnos r, y hay dos iguales, la superior y la inferior. Los puntos de concurrencia de los tres flujos son: el c para la parte superior y el d para la parte inferior. Luego, las ff.mm.mm. comprendidas entre esos dos puntos, y correspondientes a cada una de las tres ramas, deben sumarse. Cada f.m.m. está dada por el producto del flujo y la reluctancia magnética, según sabemos, con lo que se tiene, considerando el orden de las ramas indicado en la figura:
Reluctancia rama 1: R + ½ r + ½ r = R + r
Reluctancia rama 2: R
Reluctancia rama 3: R + ½ r + ½ r = R + r
Que resultan distintas, pues la rama primera y tercera tienen mayor reluctancia magnética que la rama central o N° 2. Los tres flujos son iguales, pues el sistema de tensiones aplicado a las tres bobinas primarias está formado por tres tensiones iguales desfasadas 120º, luego, multiplicando el flujo por cada reluctancia tenemos:
F1 = f1 (R + r) (1)
F2 = f2 * R (2)
F3 = f3 (R + r) (3)
En cada instante, como corresponde a un sistema trifásico normal, dos vectores tienen un sentido y el tercero tiene sentido contrario, es decir, que podernos suponer a la rama central con sentido contrario a las laterales. Hemos llamado a cada f.m.m: con la letra F, y con el subíndice qué corresponde a su rama y colocamos los mismos subíndices al flujo, para contemplar el hecho que, siendo alternados, tienen distintos valores instantáneos en magnitud y sentido. Si hacernos la suma de las ff.mm.mm. para la mitad izquierda del núcleo, para contemplar el efecto de la rama central sobre las laterales y viceversa, se tiene:
F1 - F2 = f 1 (R + r) - f 2 R (4)
Que se ha obtenido restando las ecuaciones (1) y (2), y que ha resultado una resta puesto que la segunda debe tener sentido contrario a la primera. Si hacemos lo mismo con las ecuaciones [3] y [4], se tiene:
F3 – F2 = f 3 (R + r) - f 2 R (5)
Ahora estamos en presencia de un par de ecuaciones, la [4] y la [5], que nos permitirán hacer algunas deducciones. El objeto de haberlas planteado, es para poder encontrar nuevas ecuaciones que dan las ff.mm.mm. en forma más conveniente para su interpretación.
Para disponer de otras ecuaciones que nos serán de utilidad, digamos que la suma de los valores de los tres flujos y las tres ff.mm.mm. debe ser constantemente nula, lo que ya sabemos, pero que escribimos así:
F1 + F2 + F3 = 0 (6)
f1 + f 2 + f3 = 0 (7)
Y que nos permitirán reemplazar la suma de dos de estos valores por el tercero con signo cambiado, cuando nos sea necesario.
Para operar, restemos las dos ecuaciones (4) y (5), que nos dan:
F1 – F3 = f1 (R + r) - f3 (R + r) (8)
Y ahora sumamos esas mismas ecuaciones, con lo que se tiene:
F1 – F3 - 2F2 = f1 (R + r) - f3 (R + r) + f2 R (9)
Y ahora analicemos si tenemos los elementos necesarios para encontrar el valor de cada f.m.m. Si cambiamos en la ecuación [9] la suma de las ff.mm.mm. 1 y 3 por- F2, de acuerdo con la [6], nos queda una ecuación en la cual sólo aparece esta última f.m.m., y que puede ser ordenada así:
-3 F2 = (R + r) (f 1 - f3) - 2 f2 R
Pero por la [7], la suma de los dos flujos dentro del paréntesis puede ser cambiada por el flujo de la rama 2, con signo cambiado, y finalmente resulta:
F2 = f2* R + (1/3) * f2 r (10)
Ahora tenemos el valor de la f.m.m. de la rama 2, dado como suma vectorial de dos cantidades. Encontremos los valores de las otras dos ff.mm.mm. Para ello, reemplazamos la ecuación [10] en la [9] en lugar de F2, y disponemos de una ecuación que nos da la suma de las dos ff.mm.mm. La ecuación. [8] nos da la diferencia de esas mismas ff.mm.mm., de manera qué se puede obtener cada una de ellas por simple proceso algebraico. Sumando y dividiendo por 2, se tiene:
F1 = f1* R + (1/3) * f2 r (11)
Y restando y dividiendo por 2 se obtiene el valor de la otra:
F3 = f3* R + (1/3) * f2 r (12)
Las tres ecuaciones [10], [11] y [12] nos permiten conocer las tres ff.mm.mm. que estarán presentes en las ramas del núcleo, del transformador. Notamos, por de pronto, que son diferentes. Por lo tanto ahora podemos obtener los diagramas fasoriales.
Diagrama vectorial del transformador asimétrico en vacío
Sabemos, de acuerdo a la figura a que las dos ramas laterales tienen mayor reluctancia que la central, luego, por tener más volumen serán mayores sus pérdidas por histéresis y corrientes parásitas. La corriente de vacío del transformador es igual a la suma vectorial de la magnetizante y de la que cubre esas pérdidas; esta última componente está en fase con la tensión, de modo que en el diagrama vectorial de la figura 4 hemos tomado en fase con cada una de las tres tensiones la respectiva parte de la corriente de vacío que llamábamos IP.
La que corresponde a la rama central, la N° 2, es más pequeña que las otras dos por lo que hemos dicho más arriba. Si hacemos la suma vectorial de las tres corrientes en el diagrama de la figura b, vemos que la resultante no es nula, como correspondería a un sistema trifásico perfecto. En efecto, sumando OA con O C, se tiene el vector O D, al que sumamos el O B, que tiene sentido contrario, por lo que se resta y nos queda como resultante final el vector O F, pues el D F es igual a O B. De modo que el vector O F es la corriente Ir, resultante vectorial de las tres corrientes de pérdidas del transformador.
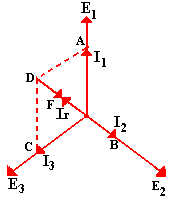
Figura 4 Diagrama vectorial de las corrientes de pérdidas en un transformador trifasico.
Como habiendo una resultante no se anularán las 3 ff.mm.mm. de las corrientes de pérdidas, tendremos que esta corriente resultante producirá una cierta cantidad de ampervueltas, y con ello, una f.m.m., de valor proporcional Ir y en fase con ella.
La figura 5 muestra el diagrama vectorial completo de un transformador trifásico en vacío, mostrando los efectos de las corrientes de perdidas Ir. Las tres tensiones y los tres flujos los hemos tomado desfasados entre sí de 120° y formando cada flujo un ángulo de 90° con la respectiva tensión. Además, tomamos 0 D, 0 H y 0 G sobre los vectores de flujo esos vectores representan las primeras partes de los segundos miembros de las ecuaciones [10], [11) y [12), ya conocidas. Paralelamente a O H se toman a partir de los puntos D, H y G, los segmentos que representan las segundas partes de las ff.mm.mm., según esas ecuaciones. Pero ahora hay que considerar la f.m.m. producida por Ir, que está en fase con la tensión E2. Esta f.m.m. aparece en cada rama, pero siempre paralelamente a la corriente I2, pues debe estar en fase con la corriente que la produce. Luego, desde los puntos J, M y K, que son los extremos adonde habíamos llegado; tomamos los vectores que representan esta nueva f.m.m., igual para las tres fases en sentido y magnitud.
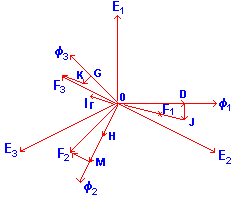
Figura 5. Diagrama vectorial completo del trafo trifasico
Haciendo ahora la suma vectorial de las tres partes de que está formada cada f.m.m. resultante de cada rama, se tienen los vectores F1, F2 y F3, que se pueden ver en la figura, y que son distintos en magnitud y dirección para cada fase. Como vemos, la asimetría del núcleo provoca un desequilibrio en las corrientes magnetizantes y en las de pérdidas (diagrama de la fig. 4), resultando que las tres corrientes totales de vacío, o las respectivas ff.mm.mn. son distintas para las tras fases.
De estas consideraciones deducimos que la potencia que absorbe en vacío un transformador trifásico será distinta para cada fase, luego no podemos hacer el ensayo en vacío para una fase sola, y multiplicar después la potencia obtenida por tres, pues se cometería un error. Para determinar las pérdidas en el hierro de un transformador trifásico, puede realizarse el ensayo en vacío como en los monofásicos, pero siempre que se mida la potencia absorbida por las tres fases simultáneamente.
En cambio, para las pérdidas en el cobre, como los bobinados de las tres fases son iguales, y las corrientes de vacío se pueden despreciar para el ensayo en cortocircuito, podemos medir las pérdidas en el cobre en una sola fase y multiplicar por tres. Para ello, según se sabe, se mide la potencia que absorbe estando el secundario en cortocircuito, y aplicando tensión reducida al primario.
Diagrama vectorial con carga
El transformador trifásico con carga puede estudiarse como si fuera un conjunto de tres transformadores monofásicos; pues cada fase forma un circuito independiente en lo que respecta a la carga, tal como sucedía en el estudio particular de las redes trifásicas. Las diferencias entre las corrientes de vacío de las tres fases del transformador, no inciden mayormente en el estado de carga, ya que sabemos que el valor relativo de tales corrientes, comparadas con las de carga, es despreciable. Puede prescindirse, pues, de considerarlo, si se trata de hacer el estudio vectorial bajo carga.
Para estudiar el comportamiento del transformador bajo carga, recurrimos al diagrama vectorial. Se dispone de un sistema de tres bobinados que se conectan a las tres ramas de una red trifásica, luego tendremos tres ff.ee.mm inducidas en esos bobinados, las que estarán a 120° entre sí. Para simplificar el diagrama consideraremos una sola fase para el trazado completo, y simplificaremos las otras dos. La figura 6 muestra el diagrama vectorial de un transformador trifásico bajo carga óhmica. Para otros tipos de carga, ya sabemos cuáles son las diferencias que se tienen en la dirección del vector corriente secundaria.
Veamos la fase N° 1, por ejemplo. El flujo es un vector que está adelantado 90° con respecto a la f.e.m. inducida E1 o E2 en los bobinados primario y secundario de esa fase. Suponemos iguales los números de espiras de ambos bobinados, para simplificar el diagrama, con lo que esas dos ff.ee.mm. serán vectores iguales. En oposición a E1 tomamos el vector -E1.
La corriente de carga secundaria es I2, y produce caídas en el bobinado secundario, en fase y en cuadratura con la tensión en los bornes V2. Descontando a la f.e.rn. esas dos caídas se tiene la tensión en los bornes. V2, del secundario. Tomando el vector opuesto a la corriente secundaria, y sumándolo vectorialmente con la corriente de vacío I0, se obtiene la corriente total primaria, I1, que se ve en la figura. Y, finalmente, sumando a la f.e.m. –E1 las dos caídas, óhmica e inductiva en el primario, que están en fase y en cuadratura con la corriente primaria, respectivamente, se tiene la tensión en los bornes, V1, para este bobinado primario de la fase N°1. Si se observa esta parte de la figura 6 y se la compara con la del transformador monofásico se vera que es idéntica.
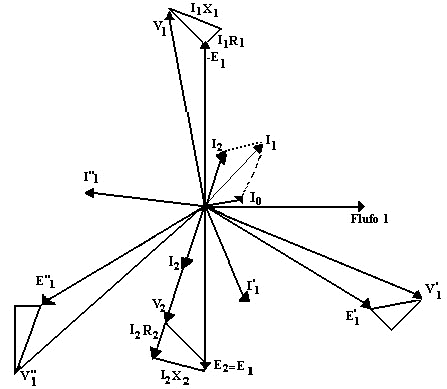
Figura. 6. - Diagrama vectorial del transformador trifásico con carga.
Si hiciéramos la misma construcción para las fases 2 y 3 se obtendría una figura simétrica, donde cada tensión primaria sería un vector apartado en 120° de los otros. Para no complicar mucho el diagrama de la figura 6, sólo se ha dibujado, en las fases 2 y 3, la f.e.m. contraria á la inducida en los respectivos primarios, que son los vectores E1' y E1". A esas ff.ee.mm. les sumamos las caídas producidas por las corrientes totales primarias I1' e I2", como se ve en la figura, con lo que se encuentran las tensiones aplicadas a los primarios de las fases 2 (V1') y 3 (V1").
En lo que antecede se ha supuesto que la carga que tomaba cada fase del transformador era la misma, lo que sucede cuando el circuito de consumo tiene sus tres ramas iguales, en lo que respecta a las impedancias conectadas. Cualquier diferencia en la magnitud o en el ángulo propio de esas impedancias produce una diferencia en las corrientes secundarias, y por ende, en las caídas de cada fase, con lo que se alterarán las tensiones en los bornes secundarios.
Para otros estados de carga, tales como los de carga inductiva o capacitiva, o los de carga asimétrica; pueden ser estudiados siguiendo las normas dadas, y comparando siempre el diagrama con los monofásicos similares, pues se repiten estos últimos tres veces, desfasados en 120°. No insistiremos pues en ello, pero recordemos que las corrientes I0 de la figura 5 son distintas para las tres fases.
Ref: Francisco L. Singer, Transformadores Industriales, Neotécnica, Buenos Aires 1976.
1.- Conexiones de transformador trifásico
Un transformador trifásico consta de tres transformadores monofásicos, bien separados o combinados sobre un núcleo. Los primarios y secundarios de cualquier transformador trifásico pueden conectarse independientemente en estrella( U ) o en delta( D ). Esto da lugar a cuatro conexiones posibles para un transformador trifásico.
1.1.- Conexión estrella( U )- estrella( U )
1.2.- Conexión estrella( U )- delta( D )
1.3.- Conexión delta( D )- estrella( U )
1.4.- Conexión delta( D )- delta( D )
1.1.- Conexión estrella( U )- estrella( U )
La conexión U -U de los transformadores se muestra en la figura 1.1.
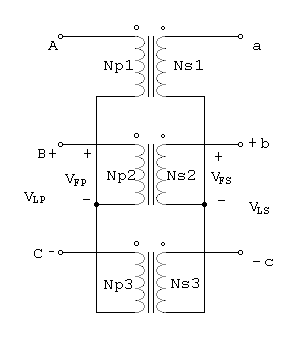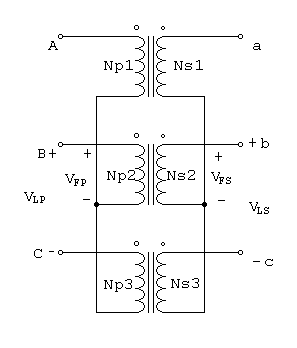
Figura 1.1 Conexión U -U
En una conexión U -U, el voltaje primario de cada fase se expresa por VFP=VLP /Ö3. El voltaje de la primera fase se enlaza con el voltaje de la segunda fase por la relación de espiras del transformador. El voltaje de fase secundario se relaciona, entonces, con el voltaje de la línea en el secundario por VLS =Ö3 * VFS. Por tanto, la relación de voltaje en el transformador es VLP / VLS = (Ö3 * VFP) / (Ö3 * VFS) = a Se emplea en sistemas con tensiones muy elevadas, ya que disminuye la capacidad de aislamiento. Esta conexión tiene dos serias desventajas.Ambos problemas del desbalance y el problema del tercer armónico, pueden resolverse usando alguna de las dos técnicas que se esbozan a continuación.
De estas técnicas de corrección, una u otra deben usarse siempre que un transformador U -U se instale. En la practica muy pocos transformadores de estos se usan pues el mismo trabajo puede hacerlo cualquier otro tipo de transformador trifásico.
1.2.- Conexión estrella( U )- delta( D)
La conexión U -D de los transformadores trifásicos se ilustra en la figura 1.2.
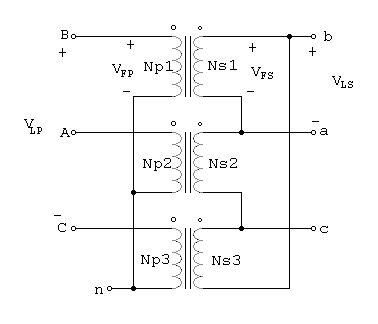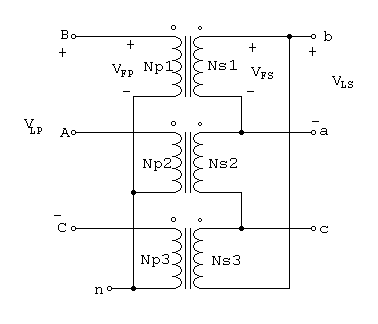
Figura 1.2 Conexión U - D
En esta conexión el voltaje primario de línea se relaciona con el voltaje primario de fase mediante VLP =Ö3 * VFP, y el voltaje de línea secundario es igual al voltaje de fase secundario VLS = VFS. La relación de voltaje de cada fase es
VFP / VFS = a
De tal manera que la relación total entre el voltaje de línea en el lado primario del grupo y el voltaje de línea en el lado secundario del grupo esVLP / VLS = (Ö3 * VFP) / VFS
VLP / VLS = (Ö3 * a)
La conexión U -D no tiene problema con los componentes del tercer armónico en sus voltajes, ya que ellos se consumen en la corriente circulatoria del lado delta(D). Está conexión también es más estable con relación a las cargas desbalanceadas, puesto que la delta(D) redistribuye parcialmente cualquier desbalance que se presente.
Esta disposición tiene, sin embargo, un problema. En razón de la conexión delta(D), el voltaje secundario se desplaza 30º con relación al voltaje primario del transformador. El hecho de que un desplazamiento de la fase haya ocurrido puede causar problemas al conectar en paralelo los secundarios de dos grupos de transformadores. Los ángulos de fase de los transformadores secundarios deben ser iguales si se supone que se van a conectar en paralelo, lo que significa que se debe poner mucha atención a la dirección de desplazamiento de 30º de la fase, que sucede en cada banco de transformadores que van a ser puestos en paralelo.
En estados unidos se acostumbra hacer que el voltaje secundario atrase al primario en 30º. Aunque esto es lo reglamentario, no siempre se ha cumplido y las instalaciones más antiguas deben revisarse muy cuidadosamente antes de poner en paralelo con ellos un nuevo transformador, para asegurarse que los ángulos de fase coincidan.
La conexión que se muestra en la figura 1.2 hará que el voltaje secundario se atrase, si la secuencia es abc. Si la secuencia del sistema fase es acb, entonces la conexión que se ve en la figura 1.2 hará que el voltaje secundario se adelante al voltaje primario en 30º .
Se usa en los sistemas de transmisión de las subestaciones receptoras cuya función es reducir el voltaje. En sistemas de distribución es poco usual (no tiene neutro) se emplea en algunos ocasiones para distribución rural a 20 KV.
1.3.- Conexión delta( D )- estrella( U )
La conexión D -U de los transformadores trifásicos se ilustra en la figura 1.3.
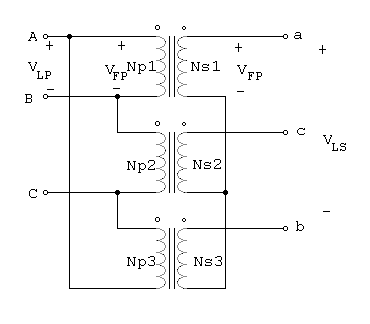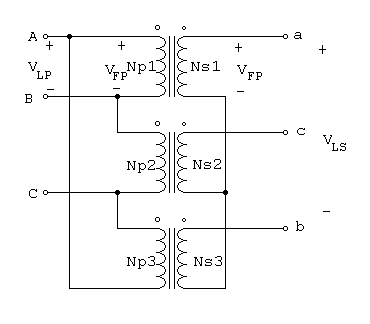
Figura 1.3 Conexión D -U
En una conexión D -U , el voltaje de línea primario es igual al voltaje de fase primario, VLP=VFP, en tanto que los voltajes secundarios se relacionan por VLS =Ö3 *VFS, por tanto la relación de voltaje línea a línea de esta conexión esVLP / VLS = VFP / (Ö
3 * VFS) VLP / VLS = a /Ö3 Esta conexión tiene las mismas ventajas y el mismo desplazamiento de fase que el transformador U -D. La conexión que se ilustra en la figura 1.3, hace que el voltaje secundario atrase el primario en 30º,tal como sucedió antes.Se usa en los sistemas de transmisión en los que es necesario elevar tensiones de generación. En sistemas de distribución industrial, su uso es conveniente debido a que se tiene acceso a dos tensiones distintas, de fase y línea.
1.4.- Conexión delta( D )- delta( D )
La conexión D-D se ilustra en la figura 1.4
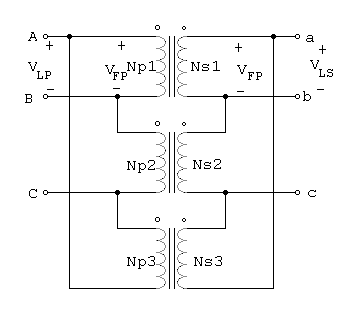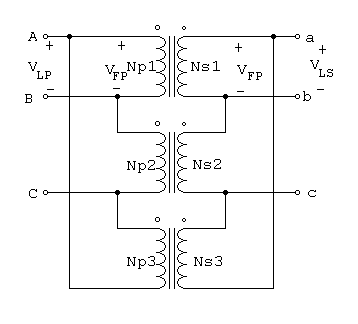
Figura 1.4 conexión D -D
En una conexión de estas,VLP = VFP
VLS = VFS
Así que la relación entre los voltajes de línea primario y secundario esVLP / VLS = VFP / VFS = a
Esta conexión se utiliza frecuentemente para alimentar sistemas de alumbrado monofásicos y carga de potencia trifásica simultáneamente, presenta la ventaja de poder conectar los devanados primario y secundario sin desfasamiento, y no tiene problemas de cargas desbalanceadas o armónicas. Sin embargo, circulan altas corrientes a menos que todos los transformadores sean conectados con el mismo tap de regulación y tengan la misma razón de tensión.
Sistemas de por unidad para transformadores trifásicos.
El sistema de medición por-unidad puede aplicarse tanto a los transformadores trifásicos como a los monofásicos. La base monófasica se aplica a un sistema trifásico en bases por fase. Si el valor total de la base voltioamperio del grupo de transformadores se llama Sbase, entonces el valor de la base voltiamperio de uno de los transformadores S1F, base es
S1F, base = Sbase / 3
Y las bases de corriente e impedancia de fase del transformador sonIF, base = S1F, base / VF, base
IF, base = S base / 3 * VF, base
Z base = (VF, base)² / S1F, base
Z base = 3 * (VF, base)² / S base
Las magnitudes de línea en los grupos de transformadores trifásicos también pueden expresarse en por-unidad. La relación entre el voltaje base de línea y el voltaje base de fase del transformador dependen de la conexión de los devanados. Si los devanados se conectan en delta, VL,base = VF,base; mientras que si la conexión se hace en estrella, VL,base=Ö3 * VF,base. La corriente de línea base en un transformador trifásico se expresa por.IL,base = S base / Ö3 * VL,base
La aplicación del sistema por-unidad en los problemas de los transformadores trifásicos es similar a su aplicación en los ejemplos para los monofásicos.
2.- Transformación trifásica con el uso de dos transformadores
Además de las conexiones usuales de los transformadores trifásicos, existen otras formas para transformar corriente trifásica con solo dos transformadores. Todas las técnicas usadas para esto se basan en la reducción de la capacidad de carga de los transformadores, que puede justificarse por ciertos factores económicos
Algunas de las principales conexiones de este tipo son:
2.1.- La conexión D abierta (o V-V)
2.2.- La conexión Y abierta - Y abierta.
2.3.- La conexión Scott-T.
2.4.- La conexión trifásica T.
2.1 - La conexión D -abierta ( o V-V )
En ciertos casos un grupo completo de transformadores puede no utilizarse para lograr transformación trifásica. Por ejemplo, supongamos que un grupo de transformadores D-D, compuesto de transformadores separados, tiene una fase averiada que se debe retirar para repararla. Si los voltajes secundarios restantes son VA = VÐ 0° y VB = VÐ 120° V, entonces el voltaje que atraviesa el intervalo en donde antes estaba el tercer transformador se expresa por
VC = - VA - VB
= VÐ0° - VÐ120° = -V – (-0.5 – j0.866)
= -0.5 + j0.866 V
VC = V Ð120° Este es exactamente el mismo voltaje que existiría si el tercer transformador aún estuviera allí. La fase C se llama fase fantasma, en algunas ocasiones. De modo que la conexión delta-abierta admite que un grupo de transformadores cumpla su función con solamente dos transformadores, permitiendo que cierto flujo de potencia continúe, aun habiéndosele removido una fase dañada.¿Cuánta potencia aparente puede suministrar el grupo, eliminando uno de sus tres transformadores? Inicialmente, parecería que puede suministrar dos terceras partes de su potencia aparente nominal, puesto que los dos tercios de los transformadores aún están presentes. Sin embargo, el asunto no es así de sencillo.
Estando conectando el grupo de transformadores D-D, (ver figura 1.4) con una carga resistiva. Si el voltaje nominal de un transformador en el grupo es VF y la corriente nominal es IF, entonces la potencia máxima que puede suministrarse a la carga es
P = 3 * VF * IF* cos q
El ángulo entre el voltaje VF y la corriente IF , en cada fase es 0°, de manera que la potencia total suministrada por el transformador es
P = 3 * VF * IF* cos0°
P = 3 * VF * IF
La conexión delta-abierta se observa en la figura 2.1
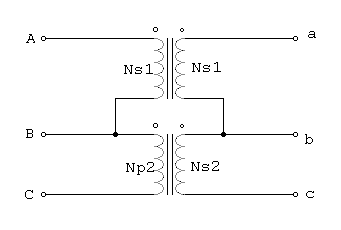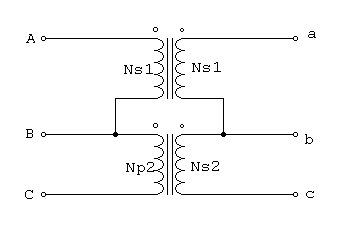
Figura 2.1 Conexión en V-V ( o delta abierta)
Es importante fijarse en los ángulos de los voltajes y corrientes en este grupo de transformadores. Puesto que falta una de las fases del transformador, la corriente de la línea de transmisión es ahora igual a la corriente de fase de cada transformador y las corrientes y voltajes del grupo difieren en un ángulo de 30°. Como que los ángulos de corriente y voltaje son diferentes en cada uno de los dos transformadores, se hace necesario examinar cada uno de ellos individualmente para determinar la potencia máxima que pueden suministrar. Para el transformador 1, el voltaje tiene un ángulo de 150°y la corriente tiene uno de 120°, así que la máxima potencia del transformador 1 se expresa mediante
P1 = VF * IF* cos(150° - 120° )
P1 = VF * IF* cos 30°
P1 = (Ö3 / 2) * VF* IF
Para el transformador 2, el voltaje está en un ángulo de 30° y la corriente en uno de 60° de modo que su potencia máxima es
P2 = VF * IF* cos(30° - 60° )
P2 = VF * IF* cos (-30° )
P 2 = (Ö3 / 2) * VF * IF
Entonces, la potencia máxima del grupo delta-abierto se expresa
P = Ö3 * VF * IF
La corriente nominal es la misma en cada transformador, aun si hay dos o tres de éstos. El voltaje también es el mismo en cada uno de ellos; así que la relación de la potencia de salida disponible en el grupo delta abierto y la potencia de salida disponible del grupo trifásico normal es
PD -abierta / P3-fases = (Ö3 * VF * IF) / (3 * VF * IF) = 1 / Ö3 = 0.577
La potencia disponible que sale del grupo en delta-abierta es sólo el 57.7% de la potencia nominal del grupo original.
Una buena pregunta que nos podríamos hacer es: ¿Qué pasaría con el resto de la capacidad nominal del grupo en delta abierta. Después de todo, la potencia total que pueden entregar los dos transformadores juntos son las dos terceras partes de la capacidad nominal del grupo original. Para averiguarlo, examine la potencia reactiva del grupo en delta abierta.
La potencia reactiva del transformador 1 es
Q 1 = VF * IF * sen (150°- 120°)
Q 1 = VF * IF * sen 30°
Q 1 = 0.5 * VF* IF
La potencia reactiva del transformador 2 es
Q 1 = VF * IF * sen (30°- 60°)
Q 2 = VF * IF * sen (-30°)
Q 2 = -0.5 * VF * IF
Así, un transformador está produciendo la potencia reactiva que el otro está consumiendo. Este intercambio de energía entre los dos transformadores es él que limita la salida al 57.7% de la potencia nominal del grupo original, en lugar del 66.7% esperado en otras condiciones.
Otra alternativa para considerar la potencia indicada de la conexión delta-abierta es que el 86.7% de la potencia nominal de los dos transformadores restantes se puede usar.
La conexión delta abierta también se emplea cuando ocasionalmente es necesario suministrar una pequeña potencia trifásica a una carga principal monofásica. En tal caso se emplean esta conexión, en la cual el transformador T2 es mucho más grande que T1.
2.2.- La conexión U abierta- D abierta.
Este tipo de conexión es muy similar a la conexión delta-abierta, con la diferencia de que los voltajes primarios se obtienen a partir de dos fases y un neutro. Esta conexión se ilustra en la figura 2.2.
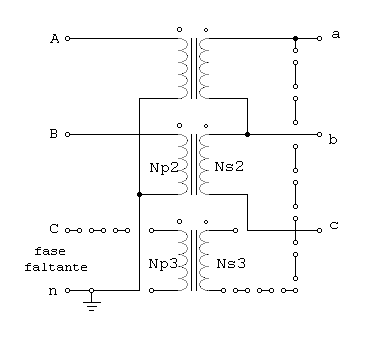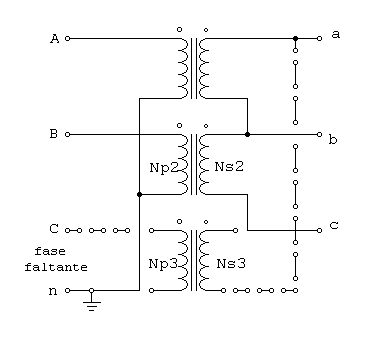
Figura 2.2 Conexión Yab-Yab
Se utiliza para dar servicio a clientes de comercio pequeños que necesitan corriente trifásica en áreas rurales en donde aun no se han instalado las tres fases en los postes de la línea de conducción. Con esta conexión, un usuario puede obtener servicio de corriente trifásica de manera provisional, hasta que con el aumento de la demanda se requiera la instalación de la tercera fase en los postes de conducción.La desventaja principal de esta conexión es que por el neutro del circuito primario debe fluir una corriente de retorno considerablemente grande.
2.3.- La conexión Scott-T.
La conexión Sott-T es la manera de obtener dos fases, separadas 90° de una fuente de alimentación trifásica. En los comienzos de la transmisión de ca, los sistemas de potencia bifásicos y trifásicos eran bastantes comunes. Por aquellos días, era una necesidad rutinaria la interconexión de sistemas de dos y tres fase, y la conexión Scott-T de transformadores se desarrollo para lograr dicho propósito.
Hoy en día la potencia bifásica esta limitada a ciertas aplicaciones de control y esta conexión se sigue utilizando para producir la potencia necesaria para su funcionamiento.
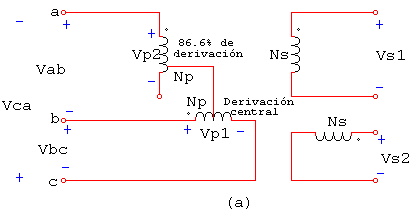
Figura 2.3. a) la conexión del transformador Scott-T
Esta conexión consiste en dos transformadores monofásicos con idéntica potencia nominal. Uno tiene derivación en su bobinado primario al 86.6% de voltaje a plena carga. Están conectados tal como se ilustra en la figura 2.3a. La derivación del transformador T2 al 86.6%, está conectada a la derivación central del transformador T1. Los voltajes aplicados al bobinado primario aparecen en la figura 2.3b y los voltajes resultantes, aplicados a los primarios de los transformadores, se ilustran en la figura 2.3c. Como estos voltajes están separados 90°, producirán una salida bifásica.
Vab = VÐ 120° Vbc = VÐ0° Vca = VÐ -120°
|
|
|
Figura 2.3. b) voltajes de alimentación trifásica; c) voltajes en los devanados primarios del transformador; d) voltajes secundarios bifásicos.
También es posible convertir potencia bifásica en potencia trifásica por medio de está conexión, pero, puesto que existen muy poco generadores bifásicos en uso, esto casi nunca se hace.
2.4.- La conexión trifásica T.
La conexión Scott T usa dos transformadores para convertir potencia trifásica en potencia bifásica a diferente nivel de voltaje. Por medio de una sencilla modificación en tal conexión, los mismos dos transformadores pueden también convertir potencia trifásica en potencia trifásica a diferente nivel de voltaje. Esta conexión se ilustra en la figura 2.4. Aquí, tanto el bobinado primario como el secundario del transformador T2 se han derivado al 86.6% y las derivaciones están conectadas a las derivaciones centrales de los correspondientes bobinados del transformador T1. En está conexión T1 se llama principal y T2 transformador excitador.
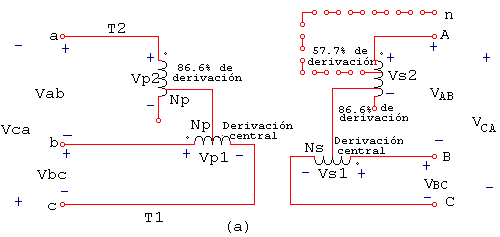
Figura 2.4 Conexión transformador trifásico T: a) Diagrama de alambrado.
Como en la conexión scott T, las tensiones de alimentación trifásicas producen dos voltajes desfasados 90° en los devanados primarios de los dos transformadores. Estos voltajes primarios producen tensiones secundarias, desfasadas también 90°. Sin embargo, a diferencia de la conexión Scott T, las tensiones secundarias se combinan para producir salida trifásica.
Vab = VÐ 120° Vbc = VÐ 0° Vca = VÐ -120°
|
|
Nota : VAB= VS2
- VS1 = (V/a) Ð 120°; VBC=
VS1 = (V/a) Ð 0°; VAB=
-VS1 - VS2 = (V/a) Ð -120° |
|
Una ventaja principal de la conexión T trifásica sobre las otras conexiones trifásicas con dos transformadores es que se puede conectar un neutro, tanto al lado primario como al lado secundario del grupo de transformadores. Esta conexión se usa algunas veces en transformadores independientes de distribución trifásica, puesto que sus costos de fabricación son más bajos que los de un grupo completo de transformadores trifásicos.
Puesto que la parte inferior de los embobinados secundarios de transformador independiente no se usa, ni en el lado primario ni en el secundario, pueden dejarse de lado sin que se modifique su comportamiento. De hecho esto es lo que ocurre en los transformadores de distribución.
Funcionamiento en paralelo
Dos transformadores trifásicos funcionaran en paralelo si tienen la misma disposición de devanados (por ejemplo, estrella-triangulo), están conectados con la misma polaridad y tienen la misma secuencia de rotación de fases. Si dos transformadores (o dos bancos de transformadores) tienen la misma tensión nominal, las mismas relación de espiras, las mismas impedancias (en porcentaje) y las mismas relaciones entre reactancia y resistencia, se repartirán la corriente de carga proporcionalmente a sus potencias nominales, sin diferencia de fase entre las corrientes de los dos transformadores. Si cualquiera de las condiciones anteriores no se cumple, la corriente de carga puede no repartirse entre los dos transformadores en proporción a sus potencias nominales y puede haber una diferencia de fase entre las corrientes en los dos transformadores.
Ref: Stephen J. Chapman, Máquinas Eléctricas (2° edición), McGraw-Hill,1993.
ENSAYOS DE TRANSFORMADORES TRIFASICOS
Hay pocas diferencias entre los transformadores trifasicos y monofasicos, en lo que respecta a los ensayos a realizar. Por lo pronto, las especificaciones sobre temperatura, aislación, etc., no pueden ser diferentes, pues las normas no hacen distingos sobre el numero de fases.
Para las caídas de tensión y regulación, también pueden estudiarse como si se tratara de uno monofasico, con solo considerar separadamente cada fase. Ya sabemos como se combinan los resultados para hacer un diagrama unico, trifasico. De modo que la característica de carga o externa, que da la tensión en los bornes secundarios al variar la carga, se tomara para una fase, pues es igual prácticamente, para las otras.
Para determinar el rendimiento aparece la primera diferencia de consideración. En efecto, las perdidas en el hierro son distintas para las tres fases, cuando el núcleo es asimétrico, lo que es común. Y como para calcular el rendimiento había que medir las perdidas en el hierro y en el cobre, ya vemos que habrá alguna diferencia con respecto a los monofasicos. Por lo cual se realizaran los ensayos en vacío y cortocircuito.
Ensayo en vacío:
Se utiliza para encontrar las perdidas en el hierro en un transformador, pero en la forma indicada en la siguiente figura.
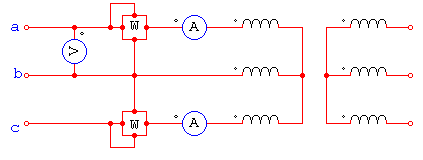
Se conectan 2 wattmetros monofasicos o uno trifásico, según el conocido metodo de medición de potencia total trifásica, un voltimetro para verificar la tensión normal, y, opcionalmente, amperímetros para poder determinar la corriente de vacío, y con ella, el ángulo de fase en vacío. Si el wattmetro es trifasico dará directamente en su escala la potencia total absorbida por el transformador, pero si se trata de dos monofásicos, hay que tener cuidado con un detalle que recordaremos.
En el método de medida de los dos wattmetros, según se estudio en electricidad, se sumaban las indicaciones cuando el desfasaje entre la corriente y la tensión era menor de 60º, pues si ese ángulo era superado, había que retar ambas lectura. En un transformador en vacío, es seguro que el angula de desfasaje supera los 60º, por lo cual hay que tener presente esta circunstancia, restando las lecturas de ambos instrumentos.
Finalmente, la potencia total de vacío representa las perdidas en el hierro de todo el transformador, y el ángulo de desfasaje de la corriente de vacío será:
Cos j = W0 / (Ö3 * V * I0)
Debiendo tenerse presente que el ángulo cuyo coseno da la ultima formula, no es el que corresponde a una fase particular, sino que a un intermedio entre las tres fases, ya sabemos que son distintos. Para tener el valor exacto de cada uno, habría que conectar tres juegos de instrumentos, uno en cada fase, y calcular el angulo por el método de medida que se conoce y que se vio en la sección correspondiente a los monofásicos.
Ensayo en cortocircuito:
Se utiliza para determinar las perdidas en el cobre, pero en este caso no es menester medir las pérdidas en las tres fases, pues como son iguales en todas, basta medir en una fase y multiplicar por tres. Se emplea el esquema que se muestra en la siguiente figura.
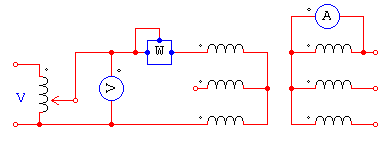
Tal como se vio en ensayo para transformadores monofásicos, hay que aplicar al primario una tensión reducida, que se gradúa de manera de tener en el secundario la carga normal, acusado por el amperímetro. El wattmetro indica la potencia que absorbe una fase del transformador con secundario en cortocircuito. Las perdidas totales en el cobre se calculan multiplicando esa lectura por tres.
Y una vez que conocemos las perdidas totales en el hierro y en el cobre de nuestro transformador trifásico, para determinar el rendimiento no hay más que conocer la potencia normal secundaria y aplicar la siguiente formula
h = W2 / (W2 + Pf + Pc)
Donde W2 es la potencia total trifásica para el secundario, en watt.
Pf son las pérdidas totales en el hierro
Pc pérdidas totales en el cobre
Para tener el rendimiento en porcentaje, vasta multiplicar el resultado por 100.
Ref: Francisco L. Singer, Transformadores Industriales, Neotécnica, Buenos Aires 1976.
TRANSFORMADOR TRIFASICO EQUILIBRADO
Circuitos equivalentes monofásicos para condiciones de equilibrio
Cuando los transformadores son exactamente iguales y las corrientes y tensiones están equilibradas, solo podrá distinguirse una fase de otra por los desfasajes de 120º entre sus corrientes y entre sus tensiones. Por tanto, las corrientes y tensiones de cada fase pueden determinarse analizando una fase cualquiera. Para estos fines suele ser conveniente considerar todos los generadores, devanados de transformadores y cargas, como si estuvieran conectados en estrella. Así, las admitancias de excitación e impedancias equivalentes de un transformador conectado en triángulo, pueden sustituirse por sus equivalentes conectados en estrella, dados por las ecuaciones incluidas en la sección de circuito equivalente (6-11), las cuales, para transformadores exactamente iguales, se reducen a
YY = 3 YD
ZY = (1/3) ZD
En donde el subíndice D indica la admitancia o impedancia de la fase del triángulo y el subiíndice U el valor equivalente en la fase de la estrella. Para condiciones de equilibrio, los puntos neutros de todos los circuitos equivalentes conectados en estrella pueden considerarse conectados directamente.
Ref: M.I.T., Circuitos Magnéticos y Transformadores, Reverté, Buenos Aires 1981.
TRANSFORMADOR TRIFASICO DESEQUILIBRADO
Todo lo anterior se ha dedicado principalmente al análisis del comportamiento de bancos simétricos de transformadores en circuitos trifásicos equilibrados. A continuación vamos a estudiar problemas prácticos en los que intervienen condiciones de desequilibrio que pueden deberse a una asimetría del banco o a cargas monofásicas no equilibradas o a cortocircuitos.
El método de las componentes simétricas resulta casi indispensable para el análisis de condiciones de desequilibrio en las cuales jueguen un papel importante las impedancias de máquinas rotativas. La mayoría de los problemas en los que los principales factores reguladores son las impedancias de los bancos de transformadores pueden, en cambio, resolverse satisfactoriamente combinando la teoría del transformador único con las relaciones entre tensiones e intensidades en circuitos trifásicos. A continuación y como repaso, se resume la teoría simplificada del transformador y las ecuaciones de los circuitos trifásicos.
Ecuaciones del transformador: Corrientemente, pueden despreciarse las corrientes de excitación de los transformadores y suponer que las corrientes de primario y secundario crean fuerzas magnetomotrices iguales y opuesta. Así, la relación entre los vectores representativos de la corriente de primario I1 y la corriente de secundario directamente opuesta IL es:
IL = a * I1 (1)
donde a es la razón N1 / N2 de los números de espira.
La relación entre las tensiones de primario y secundario es:
V1/a = V2 + IL Zeq2 (2)
donde Zeq2 es la impedancia equivalente referida al secundario. O bien, la ecuación de las tensiones del primario es:
V1 = aV2 + IL Zeq1, (3)
donde Zeq1 es la impedancia equivalente referida al primario.
El transformador, pues, está caracterizado por la ecuación (1) y por la (2) o la (3).
Ecuaciones de tensiones de línea: La suma vectorial de las tensiones entre línea y línea tomadas en orden cíclico es nula:
VAB + VBC + VCA = 0 (4)
Vab + Vbc + Vca = 0 (5)
Donde los subíndices en mayúsculas indican las fases de los primarios y los subíndices en minúsculas, las fases de los secundarios.
Ecuaciones de las tensiones de la estrella: Las relaciones vectoriales entre las tensiones de línea a línea y las tensiones de línea a neutro son:
VAB = VAN – VBN (6)
VBC = VBN – VCN (7)
VCA = VCN – VAN (8)
Vab = Van – Vbn (9)
Vbc = Vbn – Vcn (10)
Vca = Vcn – Van (11)
Obsérvese que de las cuatro relaciones dadas por las ecuaciones (4), (6), (7) y (8) (o por las 5, 9, 10, y 11) sólo tres son independientes, ya que cualquiera de ellas puede obtenerse de las otras tres.
Ecuaciones de las corrientes de línea en estrella : Para circuitos conectados en estrella con hilos neutros, la ecuación de las corrientes de primario es:
IA + IB + IC = IN (12)
donde IA, IB, IC son los vectores representativos de las corrientes de línea que penetran en los primarios e IN es el vector que representa a la corriente que circula por el neutro regresando al generador. Para las corrientes de los secundarios
Ia + Ib + Ic = In, (13)
donde Ia, Ib, Ic son los vectores representativos de las corrientes que circulan hacia la carga por las líneas de los secundarios, e In es el vector representativo de la corriente que regresa por el neutro procedente de la carga.
Para circuitos conectados en triángulo o para circuitos conectados en estrella sin hilos neutros,
IA + IB + IC = 0 (14)
Ia + Ib + Ic = 0 (15)
Relaciones entre las corrientes en la línea y en el triángulo: Las relaciones vectoriales entre las corrientes en la línea y en las fases del triángulo son:
IA = IAB – ICA (16)
IB = IBC – IAB (17)
IC = ICA –IBC (18)
Ia = Iba – Iac (19)
Ib = Icb – Iba (20)
Ic = Iac – Icb (21)
Obsérvese que de las cuatro relaciones dadas por las ecuaciones (14), (16), (17), y (18) (o por las 15, 19, 20, y 21) sólo tres son independientes, ya que cualquiera de ellas puede deducirse de las otras tres.
Como ejemplos de las aplicaciones de estas ecuaciones surgen varios problemas en relación con el empleo de bancos triángulo-triángulo, los cuales se estudian en el apartado siguiente.
Condiciones de desequilibrio en bancos triángulo-triángulo
Como la conexión triángulo-triángulo proporciona dos derivaciones entre cada par de terminales de línea tanto en el lado de los primarios como en el lado de los secundarios, las corrientes en los transformadores dependen no solo de las corrientes que circulan por la carga, sino también de las características de los transformadores. Como consecuencia de ello existen numerosos problemas en los que interviene el funcionamiento de bancos triangulo-triángulo bajo condiciones de desequilibrio debidas a cargas desequilibradas, o a asimetrías del banco ocasionadas por razones de transformación o impedancias equivalentes desiguales. A continuación se estudian algunos de dichos problemas.
1a. Corrientes circulantes en bancos triángulo-triángulo, debidas a razones de transformación desiguales. Las desigualdades en las razones de transformación de los tres transformadores originan corrientes circulantes en los bancos triángulo-triángulo. Estas corrientes puede calcularse fácilmente aplicando el teorema de Thévenin.
Consideremos el banco de transformadores de la figura 7a, en el cual los primarios están conectados en triángulo y los secundarios están conectados en serie, preparados para ser conectados en triángulo. Puede completarse el triángulo de secundarios cerrando el interruptor K.
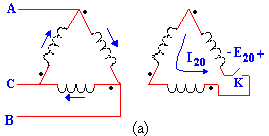
Figura 7a . Corrientes circulantes en bancos triángulo-triángulo
Si son iguales las razones de transformación de los tres transformadores, entre los extremos del interruptor abierto K no habrá tensión alguna (si se desprecian los terceros armónicos por débiles) y por tanto, al cerrar el interruptor K no circulara corriente alguna (salvo una débil corriente de excitación de la frecuencia del tercer armónico). En cambio, si no fueran iguales las razones de transformación, entre los extremos del interruptor K aparecería una tensión E20, igual a la suma vectorial de las tensiones en circuito abierto de los secundarios; es decir,
E20 = (VAB / aAB) +(VBC / a BC) +(VCA / a CA), (22)
Donde aAB,aBC, aCA son las razones de transformación N1 /N2 de los tres transformadores y son muy aproximadamente iguales a las razones de tensiones en circuito abierto. Al cerrar, en este caso, el interruptor K, se origina una corriente en los secundarios. Por el teorema de Thévenin, esta corriente en los secundarios tiene una intensidad igual al cociente entre la tensión en circuito abierto E20 y la impedancia medida en el vértice abierto del triángulo, estando cortocircuitadas las tensiones aplicadas VAB, VBC, VCA. De la figura 7b resulta evidente que la impedancia es igual a la suma vectorial de las impedancias en cortocircuitos ZSC2 del transformador medidas desde sus terminales de secundarios con los terminales de los primarios cortocircuitados.
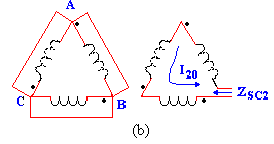
Fiura 7b. Conexión para obtener la impedancia ZSC2
Así, la corriente circulante I20 en el triángulo de secundarios es
I20 = E20 / S ZSC2 (23)
Pueden ahora determinarse las corrientes que circulan por el triángulo de primarios mediante la ecuación (1); por ejemplo,
IAB = I20 / aAB (24)
Las corrientes que circulan por las líneas de los primarios vienen dadas por las ecuaciones (16), (17) y (18); por ejemplo,
IA = IAB – ICA = (I20 / aAB) – (I20 / aCA) = ((aCA – aAB) / (aAB* aCA))* I20 (25)
Obsérvese que la corriente circulante I20 está limitada por las impedancias en cortocircuito que son relativamente pequeñas, y en consecuencia, desigualdades más bien pequeñas de las razones de transformación pueden traducirse en corrientes circulantes por el banco relativamente intensas. Así, pues convendrá evitar la conexión triangulo-triángulo de transformadores con equipo de tomas, en el caso en que los cambiadores no funcionaran simultáneamente.
Observase también que, aun cuando las corrientes circulantes por el interior del banco pueden ser relativamente intensas, las corrientes que circulan por las líneas pueden ser débiles, ya que dependen de las diferencias entre dos razones de transformación, según indica la ecuación (25). Por tanto, pueden existir en un banco corrientes circulantes relativamente intensas sin que pueda detectarse su presencia con medidas de las corrientes de línea.
1b. Ecuaciones generales para bancos triángulo-triángulo; razones de transformación iguales. Si se desprecian las corrientes de excitación, las corrientes de los primarios son iguales o las directamente opuestas de los secundarios, cuando ambas se refieren a un mismo lado. Así, si los tres transformadores tienen la misma razón de transformación a,
Iba = a* IAB (26)
Icb = a* IBC (27)
Iac = a* ICA (28),
donde IAB, IAB, IAB son los vectores representativos de las corrientes de primario en el sentido del tornillo directo respecto al flujo positivo e Iba, Icb, Iac son los vectores que representan las corrientes de secundario directamente opuestas.
Cuando se desprecian las corrientes de excitación, las ecuaciones para las tensiones son:
VAB = aVab + IAB ZAB (29)
VBC = aVbc + IBC ZBC (30)
VCA = aVca + ICA ZCA (31),
Donde ZAB, ZBC, ZCA son las impedancias equivalentes de los transformadores referidas a los lados de los primarios. Estas ecuaciones para las tensiones pueden referirse también a los lados de los secundarios. Como la suma de las tensiones de línea es igual a cero (ecs 4 y 5), la suma de las ecuaciones (29), (30), (31) indica que,
IAB ZAB + IBC ZBC + ICA ZCA = 0 (32)
Si se refieren a los secundarios las corrientes e impedancias, se tiene una relación análoga; es decir,
Ibc Zab + Icb Zbc + Iac Zca = 0, (33)
donde las impedancias Zab, Zbc, Zca están referidas a los secundarios.
Pueden ahora determinarse las tensiones e intensidades para condiciones de funcionamiento cualesquiera. Por ejemplo, supongamos que se dan vectorialmente dos de las tensiones de línea de los secundarios y dos de las intensidades de línea de los secundarios. Pueden determinarse entonces la tercera tensión de línea de los secundarios y la tercera intensidad de línea de los secundarios, puesto que la suma vectorial de las tensiones de línea es nula (ecuación 5) y también lo es la suma vectorial de las intensidades de línea (ecuación 15). Pueden entonces determinarse las corrientes sustituyendo en la ecuación (33) los valores
Iac = Iba - Ia (34)
Icb = Ib + Iba (35)
obtenidos de las ecuaciones (19) y (20). El resultado es:
Iba Zab + (Ib + Iba)Zbc + (Iba - Ia)Zca = 0, (36)
o sea,
Iba = (IaZca - Ib Zbc) / Zab + Zbc + Zbc (37)
Las otras corrientes de los secundarios pueden determinarse de manera análoga. Entonces se conocen las corrientes de los primarios a través de las ecuaciones (26), (27) y (28) y pueden determinarse las tensiones de los primarios mediante las ecuaciones (29), (30) y (31).
El examen de la ecuación (37) indica que las corrientes que circulan por los transformadores dependen de sus impedancias equivalentes. Así, si están equilibradas las corrientes de línea, no lo estarán las de los transformadores a menos que sean iguales sus impedancias complejas. En general, el transformador de menor impedancia equivalente conduce la corriente más intensa, comportándose el banco en este aspecto en forma parecida a como lo hacen las impedancias derivadas.
Así, pues, si tres transformadores conectados en triángulo-triángulo tienen iguales potencias nominales pero distintas impedancias equivalentes y suministran potencia a una carga equilibrada, el banco no puede suministrar su potencia total sin que la corriente supere su intensidad nominal en el transformador de menor impedancia equivalente.
Por esta razón es preferible utilizar transformadores exactamente iguales en las conexiones triángulo-triángulo cuando está equilibrada la carga, aun cuando pueda convenir no hacerlo si la carga está desequilibrada.
Corrientes monofásicas en bancos trifásicos.
Las cargas monofásicas casi siempre están alimentadas por sistemas trifásicos y además, como en estos sistemas pueden producirse cortocircuitos monofásicos, suele ser necesario determinar la distribución de corriente monofásicas en bancos trifásicos de transformadores.
En la figura 8 pueden verse un cierto numero de montajes trifásicos de transformadores que alimentan cargas monofásicas. Los devanados de los transformadores están representados por líneas gruesas, dibujándose paralelos entre sí los devanados primario y secundario de un mismo transformador e indicándose mediante un punto los terminales de primario y secundario de la misma polaridad. Las corrientes resultantes (despreciando las corrientes de excitación) están indicadas por flechas, representando cada flecha una unidad de intensidad sobre la base de una razón de transformación 1:1. En a),b), c), d), y e) las distribuciones de corrientes están fijadas únicamente por las conexiones de los transformadores y están determinadas por el hecho de que, si circula corriente por el secundario de algún transformador, por su primario deberá circular una corriente igual y contraria (sobre la base de una razón de transformación 1:1 y despreciando las corrientes de excitación). En a), b). c), y d) los secundarios están conectados en estrella y por tanto la corriente monofásica del secundario sólo podrá circular por un camino serie, pero en e) los secundarios están conectados en triángulo y la corriente monofásica del secundario se divide entre los dos caminos en paralelo ba y bca.

Figura 8. a), b), c) y d). Corrientes monofásicas en bancos trifásicos
Como en e) las corrientes que circulan por secundarios ba y ca de los transformadores son iguales, sus corrientes de primario deben ser, también, iguales. Las intensidades INB e INC de las corrientes de retorno del generador a través de los transformadores B y C deberán ser, también, iguales cada una a la mitad de la intensidad IAN de la corriente del transformador A, según indican las flechas en e).
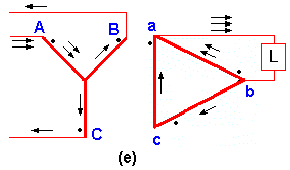
Figura 8e. Corrientes monofásicas en banco estrella-delta
Así pues, las intensidades Iba e Ica de las corrientes de secundario de los transformadores B y C también serán la mitad de la intensidad Iba de la corriente que circula por el secundario del transformador A. El transformador A, por tanto, suministra los dos tercios de la intensidad I de la corriente de carga monofásica y los transformadores B y C suministran ambos el tercio restante, según indican las flechas en e).
En la figura -8f que presenta la conexión estrella-estrella de transformadores monofásicos con neutro de primarios aislados- si circula corriente por el primario de uno de los transformadores debe regresar al generador a través de los primarios de los otros dos y por tanto la corriente monofásica que puede suministrarse entre línea y neutro en el lado de los secundarios queda limitada a una intensidad pequeña determinada por las características de excitación de los dos transformadores descargados.
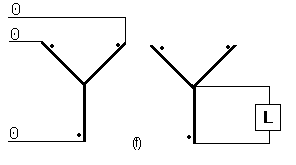
En el banco triángulo-triángulo de la figura 8g existen caminos paralelos tanto en los circuitos de primarios como en los de secundarios y la distribución de la corriente monofásica entre los transformadores no sólo está determinada por las conexiones, sino que depende de las impedancias equivalentes de los transformadores.
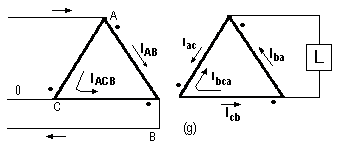
Figura 8g. Corriente monofásica en banco delta-delta.
La corriente, pues, está suministrada en parte por el transformador ba y en parte por el camino bca consistente en la combinación serie de los transformadores bc y ca en paralelo con el transformador ba. La corriente que circula por la línea c de secundario es nula y, examinando la figura 8g,
Iac = Icb = - Ibca (38)
donde Ibca es la corriente que circula de b hacia a por el camino bca. Sustituyendo la ecuación (38) en la (33) se tiene:
Iba Zab + Ibca(Zbc + Zca) = 0, (39)
de donde
Iba / Ibca = (Zbc + Zca) / Zab (40)Es decir, las intensidades son inversamente proporcionales a las impedancias equivalentes de los caminos derivados ba y bca a través del banco de transformadores. Si estos son exactamente iguales, dos tercios de la carga está alimentada por el transformador ba y un tercio por los transformadores bc y ca en serie, tal como se indica en h).
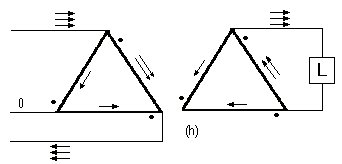
Figura 8h. Corriente monofásica en banco delta-delta.
Otro circuito en el que existen caminos derivados en los lados de los primarios y en los de los secundarios, es la conexión estrella-triángulo con el neutro de los primarios conectados al generador, como indica la figura 8i.
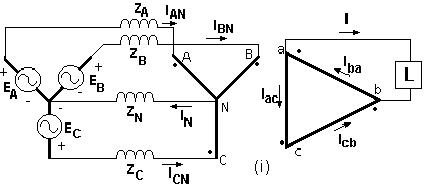
Figura 8i
En este circuito, la distribución de las corrientes depende de las impedancias, no sólo de los transformadores, sino también del generador. La ecuación para las corrientes de los primarios es:
IAN + IBN + ICN = IN (41)
Si se desprecian las corrientes de excitación, las relaciones entre las corrientes directamente opuestas de primario y secundario son:
Iba = a IAN (43)
Icb = a IBN (44)
Iac = a ICN (45)
donde a es la razón de transformación. Como la línea c de los secundarios está abierta.
Icb = Iac (46)
La relación entre la intensidad I de la corriente suministrada a la carga y las de la corrientes que circulan por los secundarios de los transformadores es:
I = Iba - Iac (44)
Sean EA, EB, EC, los vectores representativos de las fuerzas electromotrices del generador y sea ZN la impedancia compleja en el hilo neutro. Sean, también, ZA, ZB, ZC las impedancias complejas de cada fase de primarios, siendo estas impedancias las sumas vectoriales de las impedancias del generador, de la línea y equivalente del transformador referida a su lado de primarios. Las ecuaciones de las tensiones para las tres fases son:
EA = IAN ZA + IN ZN + a Vab (45)
EB = IBN ZB + IN ZN + a Vbc (46)
EC = ICN ZC + IN ZN + a Vca (47)
donde Vab, Vbc, Vca son los vectores representativos de las tensiones entre terminales de los secundarios. Obsérvese que, puesto que son tensiones entre línea y línea, su suma vectorial es nula, o sea,
Vab + Vbc + Vca = 0, (50)
Las ecuaciones números (41) a (50), ambas inclusive, constituyen las relaciones generales para un banco estrella-triángulo con una carga monofásica. Cuando, sean desiguales las impedancias o estén desequilibradas las tensiones EA, EB, EC, del generador podrá resolverse ese sistema de diez ecuaciones que contiene constantes del circuito y 14 vectores representativos de tensiones y corrientes, si se conocen las constantes del circuito y cuatro vectores independientes representativos de tensiones o intensidades. La solución general es más bien complicada.
No obstante, si las tensiones EA, EB, EC, de los generadores están equilibradas y son iguales las impedancias ZA, ZB, ZC, se simplifican mucho las relaciones entre las intensidades de corriente. Si están equilibradas las tensiones del generador, su suma vectorial es nula y como también lo es la suma de las tensiones entre terminales de los secundarios (ec. 50), la suma de las ecuaciones (47), (48), y (49) es:
0 = (IAN + IBN + ICN) Z + 3 IN ZN (51)
donde Z es la impedancia de cada fase de primario. Pero la suma vectorial de las intensidades de línea de los primarios es igual a la intensidad IN de la corriente que circula por el neutro (ec. 41). Así, de la ecuación (51) resulta,
0 = IN(Z+ 3 ZN )
o sea
IN = 0
Luego, con tensiones de generador equilibradas e impedancias de las fases de los primarios iguales, por el hilo neutro no circula corriente y por tanto la distribución de corrientes es la misma que se tendría si se desconectara el hilo neutro de los primarios. En la figura 8e puede verse esta distribución.
Ref: M.I.T., Circuitos Magnéticos y Transformadores, Reverté, Buenos Aires 1981.
Avería de la línea a tierra en el lado de los primarios de un banco estrella-triángulo con neutro a tierra
En la figura 9 se presenta otra situación en la que existen corrientes monofásicas en un banco estrella-triángulo. En ella puede verse un banco estrella-triángulo con neutro a tierra situado en el extremo receptor de una línea de transmisión, existiendo un fallo F de línea a tierra en el conductor C de fase.
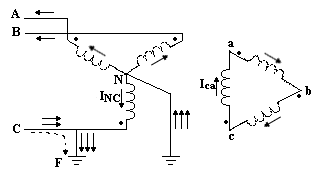
De momento, supongamos que el neutro de la estrella es la única tierra del sistema aparte de la avería. La corriente de la avería circula de la fase C a tierra y vuelve al sistema de transmisión a través de la conexión a tierra del neutro de la estrella. Como parte de esta corriente circula desde el neutro de la estrella a través del primario del transformador C, como indica la corriente I NC de la figura 9, por el secundario del transformador C deberá circular una corriente directamente opuesta Ica que también circulará por los secundarios de otros dos transformadores, según indican las flechas de la figura 9. Por tanto, por los primarios de los transformadores B y C deberán circular también corrientes directamente opuestas. Como por los tres secundarios circula la misma corriente, las tres corrientes que circulan por los primarios deberán ser de igual intensidad y estar en concordancia de fase y por tanto, cada una de ellas deberá ser la tercera parte de la corriente de la avería. La distribución de corrientes es, pues, la indicada por las flechas de trazo continuo de la figura 9, en donde cada flecha representa un tercio de la corriente en la avería. En la terminología de las componentes simétricas, estas corrientes de igual intensidad y en concordancia de fase se llaman corrientes de secuencia cero.
Análisis de componentes simétricas.
Los métodos simples estudiados en las secciones anteriores permiten resolver satisfactoriamente problemas sencillos en los que las impedancias del transformador son los principales factores rectores. Sin embargo, en problemas más complicados tales como aquellos en que intervienen impedancias de líneas de transmisión y de máquinas rotativas suele ser más expeditivo método de las componentes simétricas. Si se dispone de un analizador de redes y si la complejidad del sistema abona su empleo, puede determinarse experimentalmente el comportamiento del sistema establecido adecuadamente interconectando las redes equivalentes para secuencia cero, positiva y negativa, del sistema completo. En problemas de este tipo, el primer objetivo es la determinación del comportamiento de cada una de las partes del sistema. Los transformadores juegan aquí un importante papel.
El estudio siguiente se limita al estudio de condiciones de desequilibrio resultantes de cargas desequilibradas o de cortocircuitos en uno a más puntos de un sistema que, de otra manera, sería simétrico. En un tal sistema, nada distingue una fase de otra, excepto en los puntos de desequilibrio; es decir, las impedancias de las tres fases del sistema son iguales. En consecuencia, si se descomponen las tensiones y corrientes desequilibradas en tres sistemas equilibrados de componentes –los sistemas de secuencia cero, positiva y negativa- podrá entonces analizarse el sistema como un problema de circuitos equilibrados sobre una base por fase del sistema.
Si las tensiones y corrientes antes de aplicar el desequilibrio tiene el orden de fase abc, las componentes de secuencia positiva de las tensiones e intensidades en las tres fases para condiciones de desequilibrio forman sistemas equilibrados cuyo orden de fase es abc. Las impedancias de máquinas rotativas líneas de transmisión y bancos de transformadores son las mismas para corrientes y tensiones de secuencia positiva que para condiciones de equilibrio y la red equivalente del sistema para secuencia positiva sobre una base por fase es la misma que para las condiciones de equilibrio.
Las componentes de secuencia negativa de las tensiones y corrientes en las tres fases forman sistemas equilibrados cuyo orden de fases es acb. La única diferencia entre los sistemas de secuencia positiva y negativa es su orden de fases. Las impedancias de aparatos estáticos tales, como líneas de transmisión y transformadores, son independientes del orden de las fases, y las partes de la red de secuencia negativa que las representa son las mismas que las partes correspondientes de la red de secuencia positiva. En cambio, las máquinas rotativas presentan valores de impedancia diferentes a las corrientes de secuencia positiva que a las de secuencia negativa, y ordinariamente no generan fuerzas electromotrices internas de secuencia negativa. En consecuencia, estarán representadas en la red de secuencia negativa por valores de las impedancias diferentes de los de la red de secuencia positiva, y en la red de secuencia negativa sus fuerzas electromotrices internas estarán cortocircuitadas.
Las componentes de secuencia cero de las tensiones y corriente en las tres fases, forman también sistemas simétricos, pero con una forma de simetría diferente de la existente para las componentes de secuencia positiva o negativa. Por definición, el vector representativo de la componente I0 de secuencia cero de los vectores Ia, Ib, Ic, representativos de las corrientes en las fases de un sistema trifásico es:
I0 = (1/3) * (Ia+ Ib + Ic)
Las componentes de secuencia cero de las tres corrientes son iguales y están en concordancia de fase entre sí, en contraste con lo que ocurre con las componentes de secuencia positiva o negativa que son de igual magnitud pero están desfasadas 120° ; es decir, para las componentes de secuencia cero de Ia, Ib e Ic,
Ia0 = Ib0 = Ic0
"De la ecuación anterior resulta que sólo podrán existir corrientes de secuencia cero cuando esté dispuesto el circuito de manera que la suma vectorial de las corrientes de las tres fases no sea obligatoriamente nula".
Esto significa que no podrán existir corrientes de secuencia cero en máquinas rotativas simétricas conectadas en estrella, bancos de transformadores, o líneas de transmisión a menos que se pongan a tierra o interconecten uno a más puntos neutros. Por ejemplo no podrán existir corrientes de secuencia cero en los primarios de los transformadores de la figura 9 si no estuviera puesto a tierra el punto neutro N. Como los caminos de las corrientes de secuencia cero son distintos de los de las corrientes de secuencia positiva o negativa, las impedancias a las corrientes en máquinas rotativas y líneas de transmisión son distintas de las impedancias a corrientes de otra secuencia.
Sin embargo, pueden existir corrientes de secuencia cero en las fases de circuitos conectados en triángulo. En esta disposición, las componentes de secuencia cero de las tres corrientes del triángulo, al ser iguales y estar en fase, no hacen mas que circular por el triángulo, pero no por las líneas a él conectadas, como ocurre en los devanados secundarios del banco de transformadores de la figura9. Como la suma vectorial de las tres tensiones entre línea y línea de un sistema trifásico, tomadas en orden cíclico, debe ser siempre nula, es imposible la existencia de componentes de secuencia cero en las tensiones entre línea y línea. Así pues, aun cuando en los secundarios conectados en triángulo de la figura 9 existan corrientes de cero, no crean componentes de secuencia cero en las tensiones entre línea y línea.
Del estudio anterior resulta evidente que las conexiones de los bancos de transformadores ejercen influencias importantes sobre las corrientes de secuencia cero. Los principios generales pueden resumirse de manera muy sencilla.
Pueden existir corrientes de secuencia cero en las líneas que terminan en un grupo de devanados conectados en estrella, solamente cuando el punto neutro éste a tierra o conectado a un hilo neutro. Si el punto neutro está aislado, el circuito está abierto en lo que concierne a corrientes de secuencia cero.
Las líneas terminales en un grupo de devanados conectados en triángulo están en circuito abierto en lo que concierne a corrientes de secuencia cero, ya que no existe ninguna conexión neutra que les proporcione un camino de retorno. Sin embargo, en el triángulo pueden inducirse corrientes circulantes si existen corrientes de secuencia cero en otros devanados con los que esté acoplado inductivamente el grupo conectado en triángulo.
Si se disponen los circuitos de manera que puedan existir corrientes de secuencia cero en los devanados primarios y secundario, las corrientes de secuencia cero de un lado inducen en el otro corrientes de secuencia cero que crean fuerzas magnetomotrices iguales y opuestas (despreciando las corrientes de excitación). La impedancia a las corrientes de secuencia cero introducida por dicho banco de transformadores es, pues, la impedancia equivalente, o en cortocircuito, por fase. Por ejemplo, un grupo de transformadores exactamente iguales conectados en estrella-estrella con ambos puntos neutros puestos a tierra es equivalente en la red para secuencia cero a la impedancia en cortocircuito de uno de los transformadores en serie con los circuitos primarios y secundarios (bien entendido, claro está, que todas las corrientes, tensiones e impedancias están referidas a una base común). El circuito equivalente para la secuencia cero es el de la figura10a.
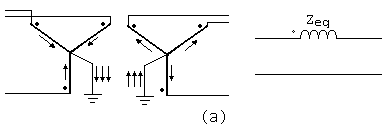
Si existieran corrientes de secuencia cero en los devanados conectados de un banco estrella-triángulo cuyo neutro de la estrella éste puesto a tierra, las corrientes de secuencia cero que circulan por el lado conectado en estrella inducen en el triángulo corrientes de secuencia cero que no harán más que circular por él, como se indica en la figura 9. Así, pues, la impedancia a la secuencia cero del banco de transformadores por fase vista desde su lado conectado en estrella es igual a la impedancia equivalente de uno de los transformadores. Sin embargo, por los circuitos exteriores conectados al triángulo no pueden circular corrientes de secuencia cero y el banco, por tanto, actúa como un circuito abierto para las corrientes de secuencia cero, situado en el circuito exterior del lado conectado en triángulo, como se indica en la figura 10b.
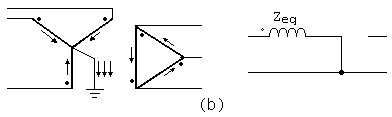
Figura 6b. Circuitos equivalente para secuencia cero.
En cambio si se disponen las conexiones de transformador de manera que puedan existir corrientes de secuencia cero en uno de los lados pero no en el otro, la impedancia a las corrientes de secuencia cero en el lado que puedan existir es la impedancia en circuito abierto o impedancia de excitación de una fase del banco. En el otro lado, el banco actúa como circuito abierto para las corrientes de secuencia cero. Esta es la situación en la disposición indicada en la figura 10c.
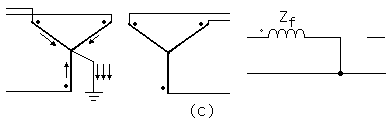
Figura 6c. Circuitos equivalente para secuencia cero.
Aplicando los principios generales ilustrados en el estudio anterior, puede determinarse la distribución de corrientes de secuencia cero en cualquier banco de transformadores que contenga una combinación cualquiera de devanados conectados en estrella y en triángulo. Estos mismos principios se aplican también a los transformadores trifásicos, igual que a los bancos trifásicos de unidades monofásicas, siendo la única diferencia que la impedancia de excitación para secuencia cero de un transformador trifásico del tipo núcleo es muy inferior a la de un banco análogo de unidades monofásicas.
Ref: M.I.T., Circuitos Magnéticos y Transformadores, Reverté, Buenos Aires 1981.