Durante el transporte de la energía eléctrica se originan pérdidas que dependen de su intensidad. Para reducir estas perdidas se utilizan tensiones elevadas, con las que, para la misma potencia, resultan menores intensidades. Por otra parte es necesario que en el lugar donde se aplica la energía eléctrica, la distribución se efectúe a tensiones más bajas y además se adapten las tensiones de distribución a los diversos casos de aplicación.
La preferencia que tiene la corriente alterna frente a la continua radica en que la corriente alterna se puede transformar con facilidad.
La utilización de corriente continua queda limitada a ciertas aplicaciones, por ejemplo, para la regulación de motores. Sin embargo, la corriente continua adquiere en los últimos tiempos una significación creciente, por ejemplo para el transporte de energía a tensiones extraaltas.
Para transportar energía eléctrica de sistemas que trabajan a una tensión dada a sistemas que lo hacen a una tensión deseada se utilizan los transformadores.
A este proceso de cambio de tensión se le "llama transformación".
El transformador es un dispositivo que convierte energía eléctrica de un cierto nivel de voltaje, en energía eléctrica de otro nivel de voltaje, por medio de la acción de un campo magnético. Esta constituido por dos o más bobinas de alambre, aisladas entre si eléctricamente por lo general y arrolladas alrededor de un mismo núcleo de material ferromagnético.
El arrollamiento que recibe la energía eléctrica se denomina arollamiento de entrada, con independencia si se trata del mayor (alta tensión) o menor tensión (baja tensión).
El arrollamiento del que se toma la energía eléctrica a la tensión transformada se denomina arrollamiento de salida. En concordancia con ello, los lados del transformador se denominan lado de entrada y lado de salida.
El arrollamiento de entrada y el de salida envuelven la misma columna del núcleo de hierro. El núcleo se construye de hierro por que tiene una gran permeabilidad, o sea, conduce muy bien el flujo magnético.
En un transformador, el núcleo tiene dos misiones fundamentales:
Para generar el flujo magnético, es decir, para magnetizar el núcleo de hierro hay que gastar energía eléctrica. Dicha energía eléctrica se toma del arrollamiento de entrada.
El constante cambio de magnetización del núcleo de hierro origina pérdidas. Estas pérdidas pueden minimizarse eligiendo tipos de chapa con un bajo coeficiente de pérdidas.
Además, como el campo magnético varía respecto al tiempo, en el hierro se originan tensiones que dan orígenes a corrientes parásitas, también llamadas de Foucault. Estas corrientes, asociadas con la resistencia óhmica del hierro, motivan pérdidas que pueden reducirse empleando chapas especialmente finas, de unos 0.3 mm de espesor, aisladas entre sí (apiladas). En cambio, en un núcleo de hierro macizo se producirían pérdidas por corrientes parásitas excesivamente grandes que motivarían altas temperaturas.
Una vez descritos los dos principales componentes, va a tomar conocimiento del principio de la transformación:
El flujo magnético, periódicamente variable en el tiempo, originado por la corriente que pasa a través del arrollamiento de entrada induce en el arrollamiento de salida una tensión que varía con la misma frecuencia.
Su magnitud depende de la intensidad y de la frecuencia del flujo así como del número de vueltas que tenga el arrollamiento de salida, como se ve en la siguiente formula (ley de la inducción).
E = 4.44 * 10-8 * aC * B * f * N
En la que aC = sección del núcleo en pulgadas cuadradas, B = densidad máxima del flujo en líneas por pulgada cuadrada, E = tensión eficaz, f = frecuencia en Hz y N = número de espiras del devanado, o bien 10-9 * aC * B * f * N, expresando aC y B en cm2.
Todo lo anterior se analiza con más detalle en las siguientes lecciones.
Ref: Herbert Nessler & Friedrich Stadelmeier, Constitución y Funcionamiento del Transformador, Siemens Aktiengesellschaft, Berlín 1988.
Un transformador ideal es un artefacto sin pérdidas, con una bobina de entrada y una bobina de salida. Las relaciones entre los voltajes de entrada y de salida, y entre la corriente de entrada y de salida, se establece mediante dos ecuaciones sencillas. La figura l muestra un transformador ideal.

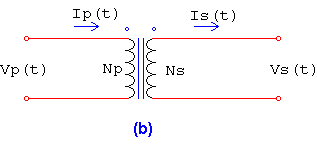
Figura 1. a) Esquema de un transformador ideal. b) Símbolos esquemáticos de un transformador ideal.
En el transformador que se muestra en la figura 1 tiene NP espiras de alambre sobre su lado primario y NS de espiras de alambre en su lado secundario. La relación entre el voltaje VP(t) aplicado al lado primario del transformador y el voltaje VS(t) inducido sobre su lado secundario es
VP(t) / VS(t) = NP / NS = a
En donde a se define como la relación de espiras del transformador
a = NP / NS
La relación entre la corriente ip(t) que fluye en el lado primario del transformador y la corriente is(t) que fluye hacia fuera del lado secundario del transformador es
NP * iP(t) = NS * iS(t)
iP(t) / iS(t) = 1 / a
En términos de cantidades fasoriales, estas ecuaciones son
VP / VS = a
IP / IS = 1 / a
Nótese que el ángulo de la fase de VP es el mismo que el ángulo de VS y la fase del ángulo IP es la misma que la fase del ángulo de IS. La relación de espiras del transformador ideal afecta las magnitudes de los voltajes y corrientes, pero no sus ángulos.
Las ecuaciones anteriores describen la relación entre las magnitudes y los ángulos de los voltajes y las corrientes sobre los lados primarios y secundarios del transformador, pero dejan una pregunta sin respuesta: dado que el voltaje del circuito primario es positivo en un extremo especifico de la espira, ¿cuál seria la polaridad del voltaje del circuito secundario?. En los transformadores reales seria posible decir la polaridad secundaria, solo si el transformador estuviera abierto y sus bobinas examinadas. Para evitar esto, los transformadores usan la convección de puntos. Los puntos que aparecen en un extremo de cada bobina en la figura1 muestran la polaridad del voltaje y la corriente sobre el lado secundario del transformador. La relación es como sigue:
1.- Si el voltaje primario es positivo en el extremo punteado de la bobina con respecto al extremo no punteado, entonces el voltaje secundario será también positivo en el extremo punteado. Las polaridades de voltaje son las mismas con respecto al punteado en cada lado del núcleo.
2.- Si la corriente primaria del transformador fluye hacia dentro del extremo punteado de la bobina primaria, la corriente secundaria fluirá hacía afuera del extremo punteado de la bobina secundaria.
Potencia en un transformador ideal
La potencia suministrada al transformador por el circuito primario se expresa por medio de la ecuación
Pent = VP * IP * cos q P
En donde q p es el ángulo entre el voltaje y la corriente secundaria. La potencia que el circuito secundario suministra a sus cargas se establece por la ecuación:
Psal = VS * IS * cos q S
En donde q s es el ángulo entre el voltaje y la corriente secundarios. Puesto que los ángulos entre el voltaje y la corriente no se afectan en un transformador ideal, q p=q s=q . Las bobinas primaria y secundaria de un transformador ideal tienen el mismo factor de potencia.
¿Cómo se compara la potencia que va al circuito primario del transformador ideal, con la potencia que sale por el otro lado?
Es posible averiguarlo por medio de las ecuaciones de voltaje y corriente. La potencia que sale de un transformador es:
Psal = VS *IS* cos q
Aplicando las ecuaciones de relación de espiras nos resulta Vs = Vp / a y Is = a * Ip así que
Psal = (VP/a) * a * IP * cos q
Psal = VP * IP * cos q = Pent
De donde, la potencia de salida de un transformador ideal es igual a su potencia de entrada.
La misma relación se aplica a la potencia reactiva Q y la potencia aparente S.
Qent = VP *IP *sen q = VS *IS *sen q = Qsal
Sent = VP *IP = VS *IS = Ssal
Transformación de la impedancia por medio de un transformador
La impedancia de un artefacto o un elemento se define como la relación fasorial entre el voltaje y la corriente que lo atraviesan:
ZL = VL / IL
Una de las propiedades interesantes de un transformador es que puesto que cambia los niveles de voltaje o corriente, también cambia la relación entre el voltaje y corriente y por consiguiente, la impedancia aparente de un elemento. Para entender mejor esta idea véase la siguiente figura 2.
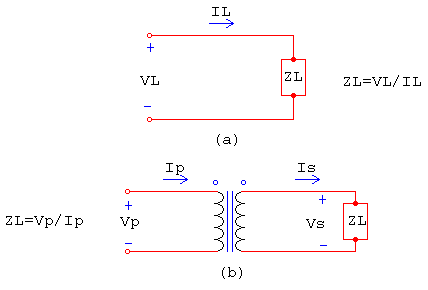
Figura 2. a) Definición de impedancia. b) Escalamiento de la impedancia a través de un transformador
Si la corriente secundaria se llama Is y el voltaje secundario Vs, entonces la impedancia de la carga total se expresa por
ZL = VS / IS
La impedancia aparente del circuito secundario primario del transformador es
Z¢ L = VP / IP
Como el voltaje primario se puede expresar
VP = a * VS
Y la corriente primaria
IP = IS / a
La impedancia del primario es
Z¢ L = VP /IP = (a * VS) / (IS /a) = a² * (VS / IS)
Z¢L = a² * ZL
Con un transformador es posible acoplar la magnitud de la impedancia de la carga con la magnitud de la impedancia de la fuente escogiendo sencillamente la relación apropiada de espiras.
Análisis de los circuitos que contienen transformadores ideales
Si un circuito contiene un transformador ideal, entonces la forma más fácil de calcular los voltajes y corrientes del circuito es reemplazar la porción del circuito de uno de los lados del transformador por uno equivalente con las mismas características terminales. Después que el circuito equivalente se ha sustituido por un lado, el circuito resultante (sin transformador) puede calcularse por sus voltajes y corrientes. En la porción del circuito que no se modificó, los resultados obtenidos serán los valores correctos de los voltajes y corrientes del otro lado del transformador. El proceso de reemplazar un lado de un transformador por su nivel de voltaje equivalente del otro lado se llama reflexión o referencia del primer lado al segundo lado.
¿Cómo se forma un circuito equivalente?
Su forma es exactamente la misma que la del circuito original. Los valores de los voltajes en el lado que se está reemplazando se escalonan por medio de la ecuación ( VP/VS = a ) y los valores de la impedancia, por medio de la ecuación ( ZL¢ =a² * ZL). Las polaridades de las fuentes de voltaje del circuito equivalente se invertirán en su dirección en el circuito original, si el punteado de las bobinas de un lado del transformador está al contrario del punteado de las bobinas del otro lado.
Ref: Stephen J. Chapman, Máquinas Eléctricas (2° edición), McGraw-Hill,1993.