La malla de tierra es un conjunto de conductores desnudos que permiten conectar los equipos que componen una instalación a un medio de referencia, en este caso la tierra. Tres componentes constituyen la resistencia de la malla de tierra:

•  La resistencia del conductor que conecta los equipos a la malla de tierra.

•  La resistencia de contacto entre la malla y el terreno.

•  La resistencia del terreno donde se ubica la malla.

Una malla de tierra puede estar formada por distintos elementos:

•  Una o más barras enterradas.

•  Conductores instalados horizontalmente formando diversas configuraciones.

•  Un reticulado instalado en forma horizontal que puede tener o no barras conectadas en forma vertical en algunos puntos de ella.

En la figura N° 5. 1 se muestra un esquema general de una malla de puesta e tierra.

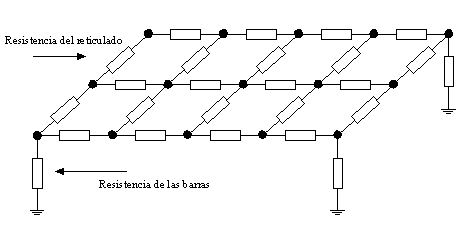
Figura N° 5. 1 Configuración general de una malla.

Las barras verticales utilizadas en la construcción de las mallas de tierra reciben el nombre de barras copperweld y están construidas con alma de acero revestidas en cobre. El valor de la resistencia de una malla de tierra depende entre otros parámetros de la resistividad del terreno. El método más usado para determinar la resistividad del terreno es el de Schlumberger, el cual permite determinar las capas que componen el terreno, como también la profundidad y la resistividad de cada uno de ellos.

5.3.1.- Objetivos de una malla.

Los objetivos fundamentales de una malla de tierra son:

•  Evitar tensiones peligrosas entre estructuras, equipos y el terreno durante cortocircuitos a tierra o en condiciones normales de operación.

•  Evitar descargas eléctricas peligrosas en las personas, durante condiciones normales de funcionamiento.

•  Proporcionar un camino a tierra para las corrientes inducidas. Este camino debe ser lo más corto posible.

5.3.2.- Tipos de mallas.

Se deben distinguir dos tipos de mallas en una instalación eléctrica que son:

•  Mallas de alta tensión.

•  Mallas de baja tensión.

Ambas mallas deben estar separadas de modo que la inducción de voltajes de la malla de alta en la de baja sea £ a 125 V, a menos que la resistencia de cada una de ellas, en forma separada, sea inferior a 1 W , en este caso pueden las mallas conectarse entre sí.

La resistencia de una malla de baja tensión, según la norma editada por la Superintendencia de Servicios Eléctricos y Combustibles (SEC) queda limitada como se muestra en la expresión (5.1).

(5.1)

Donde:

65V : valor de tensión máximo a que puede quedar sometida una persona cuando sucede un cortocircuito a tierra.

I : valor máximo de la corriente de falla monofásica, definida por la corriente de operación de las protecciones.

5.3.3.- Resistividad equivalente del terreno.

Una forma ideal de realizar cálculos de resistencia y solicitaciones de voltaje para una puesta a tierra ubicada en un terreno de 2 o más estratos, sería de disponer de una resistividad equivalente que transforme un terreno en resistividad ? 1 , ? 2 , …? n y espesores h 1 , h 2 ,…h n-1 . En un terreno homogéneo de resistividad ? eq ; esto, es un terreno que produjera los mismos valores de resistencia y las mismas solicitaciones que el terreno real.

Según el método de Burdoff-Yakobs el cual propone una equivalencia de un sistema de 3 o más estratos, a un sistema de 2 estratos, equivalente dentro de un margen aceptable.

De acuerdo con Burgsdorf-Yakobs, una puesta a tierra compuesta por un conjunto de conductores horizontales enterrados a una profundidad “h” y un conjunto de barras verticales de longitud “l”, se aproxima a una prisma metálico recto en la medida que se incrementa el número de elementos verticales y su resistencia disminuye en forma asintótica hasta un valor mínimo.

Sobre la base antes expuesta, esta equivalencia aproximada a las primeras “n” capas hasta una profundidad de “h”, queda determinado por los siguientes parámetros y expresiones [6]

(5.2)

(5.3)

(5.4)

(5.5)

(5.6)

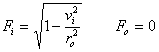(5.7)

Finalmente:

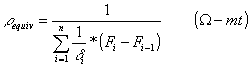(5.8)

Donde:

A : Area de la malla de puesta a tierra (m)

r : radio equivalente del área de la malla (m)

h : profundidad de la malla (m)

h i : profundidad de la capa i (m)

? : resistividad equivalente del terreno

? i : resistividad equivalente de la capa i (O-mt)

S : área que cubre el perímetro del electrodo de tierra (m 2 )

Para un terreno de 3 capas, la situación de resistividad y profundidad puede clasificarse según la figura N° 5.2.

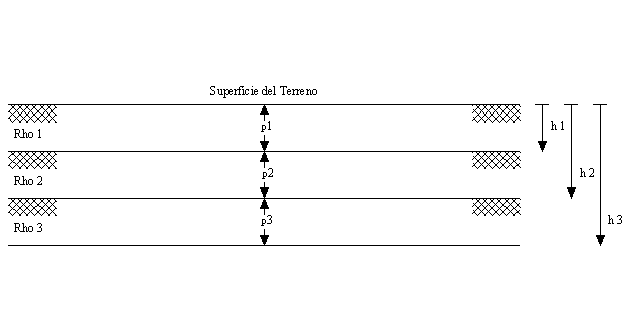
Figura N° 5.2 Configuración de un terreno de tres capas.

La resistividad equivalente de un terreno es dependiente de las dimensiones y ubicación del electrodo y se modifica si cambia su área o profundidad (tabla Nº 5.1).

Tabla Nº 5.1

Cuando se desea conocer la corriente durante un cortocircuito a tierra, es necesario que hacer uso de las mallas de secuencia. A partir de las relaciones de corriente de falla monofásica se puede realizar el circuito de la figura N° 5.3.

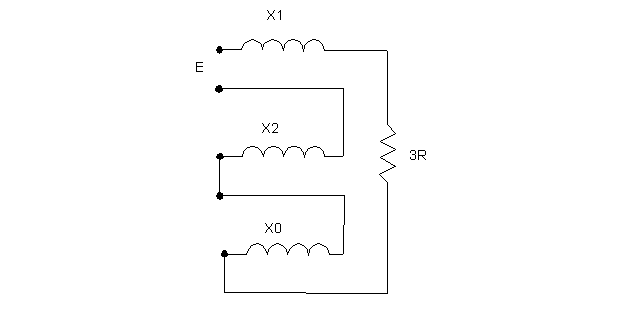
Figura N° 5.3 Conexión de mallas de secuencia considerando la resistencia de falla a tierra.

En la figura N° 5.3, R es el valor de resistencia de tierra, Io el valor de la corriente de secuencia cero. E es la tensión de fase neutro del sistema, antes de producirse el cortocircuito. Mediante un análisis de las mallas de secuencia a través de las distintas relaciones, se puede obtener finalmente la siguiente expresión.

(5.9)

Donde:

I f : Corriente de cortocircuito monofásica a tierra.

5.3.4.- Resistencia de puesta a tierra.

La resistencia de la malla de tierra de una subestación, depende del terreno en el cual se instale, la superficie de la cubierta, la resistividad equivalente del terreno, el valor de la resistencia de los electrodos, etc.

Según Schwarz, la resistencia de una malla compuesta es:

 

(5.10)

 

Donde

R 1 : Resistencia del reticulado

R 2 : Resistencia de las barras

R 12 : Resistencia mutua entre el reticulado y las barras

 

Para calcular cada una de las resistencias se utilizan las siguientes ecuaciones

 

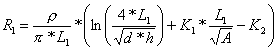(5.11)

(5.12)

(5.13)

Donde:

d : Diámetro del conductor (m)

h : Profundidad de la malla (m)

A : Area que cubre la malla (m 2 )

L 1 : Longitud total de los conductores de la malla (m)

L 2 : Longitud de los electrodos verticales (m)

? : Resistividad del terreno (Om)

n : Cantidad de electrodos verticales

r : Radio de los electrodos verticales (m)

l : Longitud de la barra (m)

 

Los factores K 1 y K 2 se calculan de acuerdo con las siguientes expresiones.

(5.14)

(5.15)

Donde:

a : Ancho de la malla (m)

b : Largo de la malla (m)

 

 

5.3.5.- Seguridad hacia las personas.

El riesgo de muerte de una persona que ha sufrido contacto con algún elemento energizado, depende de.

•  Frecuencia.

•  Magnitud.

•  Duración de la circulación de corriente a través del cuerpo humano.

El tiempo que una persona puede soportar la circulación de una corriente eléctrica a través de su cuerpo, sin sufrir daño corporal (fibrilación ventricular), es bastante corto y puede ser determinada mediante una ecuación experimental dada en la ecuación (5.16)

(5.16)

Donde:

I k : Valor eficaz máximo de la corriente a través del cuerpo humano (A)

t : Tiempo de duración del contacto (seg.)

0.116 : Constante empírica

Esta ecuación (5.16) permite determinar el potencial máximo al que puede quedar sometido una persona cuando queda sometida a una diferencia de potencial.

La ANSI/IEEE ha propuesto en su forma st.80, una serie de expresiones para el calculo aproximado de la solicitaciones de voltaje en el interior y contorno de una malla a tierra. Estas expresiones se basan en una modelación simplificada de una malla, complementada con estudios experimentales realizados en modelos (cuba electrolítica). Las proposiciones iniciales se han ido modificando en las nuevas versiones de la norma, en la medida que los métodos más exactos disponibles, han indicado diferencias importantes con los valores obtenidos de este método aproximado.

5.3.5.1.- Tensión de contacto.

La tensión de contacto es aquella a la que queda sometida una persona al tocar un equipo energizado (figura Nº 5.4).

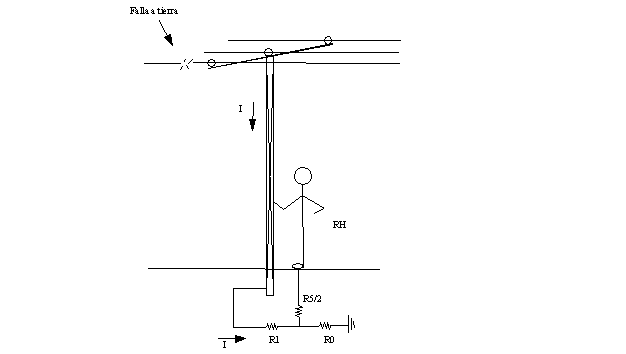
Figura N° 5. 4Tensión de contacto

La máxima tensión de contacto a que puede quedar sometida una persona se determina mediante la ecuación (5.17).

(5.17)

Donde:

: Tiempo de duración del contacto (seg.)

R p : Resistencia de contacto de un pie con el terreno

 

Una aproximación aceptada para la tensión de contacto queda determinada por la siguiente ecuación (5.18). La tensión de contacto aproximada deberá ser menor al valor máximo admisible.

(5.18)

El valor de K m y Ki se puede hallar mediante las siguientes ecuaciones

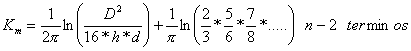(5.19)

(5.20)

Donde:

D : Distancia entre conductores paralelos (m)

h : Profundidad de la malla (m)

d : Diámetro del conductor de la malla (m)

n : Numero de conductores del lado mayor de la malla

 

 

5.3.5.2.- Tensión de paso.

 

La tensión de paso (figura Nº 5.5) corresponde a la elevación de potencial debido a la corriente de cortocircuito que circula desde la malla al terreno, y aunque a su vez forzara a que circule una corriente por el cuerpo de una persona que se encuentre parada sobre la malla. La tensión de paso se determina para una distancia entre puntos a considerar con separación de 1 metro.

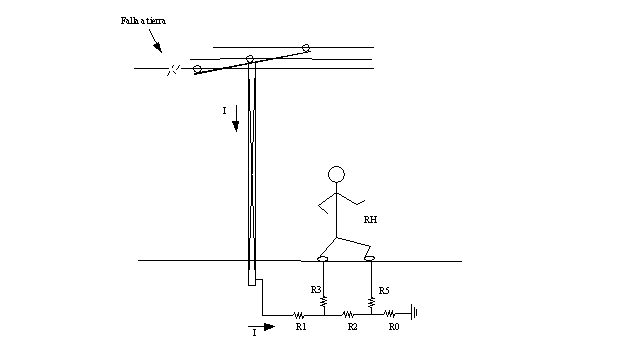
Figura N° 5.5 Tensión de paso.

 

La tensión de paso máxima a que puede quedar sometida una persona se indica en la siguiente ecuación (5.21).

(5.21)

La tensión de paso deberá ser menor al valor máximo permisible, estas expresiones quedan determinadas de la siguiente ecuación (5.22)

(5.22)

Donde:

K s : Factor de proporcionalidad debido a la geometría de la malla

K m : Factor de proporcionalidad debido a la geometría de la malla

K i : Factor de proporcionalidad del terreno en donde se instala la malla

? : Resistividad del terreno

I : Corriente dispersada por la malla de tierra

L : Longitud total equivalente de los elementos que conforman la malla, considerando conductores y mallas

t : Tiempo de operación de las protecciones

La resistencia de contacto entre un pie y el terreno, es la del calzado de la persona, mas la resistencia de contacto de éste con el terreno. La primera de ellas, se acostumbra suponerla igual a cero, considerando posibles condiciones de humedad. La resistencia de contacto de un pie en el terreno se puede determinar aproximadamente aceptando su equivalencia con una plancha circular de un radio de 8 cm.

Laurent y Heppe han propuesto para esta situación, expresiones que permiten determinar aproximadamente la resistencia de un electrodo de pequeña dimensiones en comparación con el espesor del estrato superior. Los valores calculados con estas expresiones son muy similares, siendo mas simple el cálculo con la de Laurent (5.23).

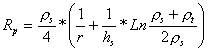(5.23)

Donde:

r : 0.08 metros

? s : Resistividad del material artificial que cubre el área de la puesta a tierra.

h s : Espesor, normalmente entre 0.10 y 0.15 metros.

? t : Resistividad superior del primer estrato natural del terreno.

En la figura N° 5.6 se indica, para h s = 0.10 y 0.15 metros, los valores de resistencia R p de contacto de un pie con el terreno. De ella se desprende que el valor de resistencia de un pie en el terreno varia, dependiendo de la resistividad del estrato superior del terreno natural, entre 1.5 y 3 veces ? s , para h s = 0.10 metros; y entre 2 y 3 veces ? s , para h s = 0.15 metros. Esto difiere del valor constante 3 ? s , tradicionalmente utilizado al no considerar el efecto del terreno bajo la capa de materia artificial.

 

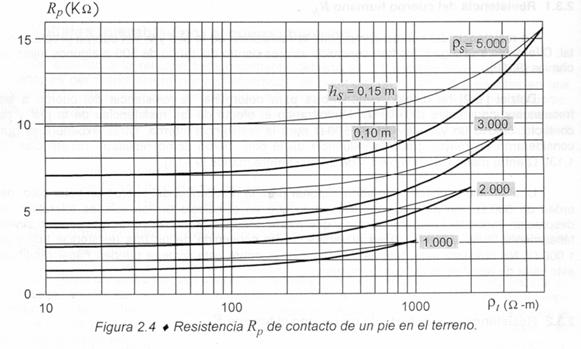
Figura N° 5.6 Resistencia R p de contacto de un pie en el terreno