Se describirán los métodos gráficos que son usados para el cálculo de valores de flecha y tensiones, ya que el determinar dichos valores, es uno de los problemas que es necesario resolver, tanto en la etapa de proyectos como de construcción de una línea. Actualmente el uso de programas computacionales, ha reemplazado aquellos métodos en la parte de cálculo, ya que la base teórica es la misma que la de los métodos gráficos.
2.9.2.- Planteamiento de la ecuación de la flecha 
Un conductor de peso uniforme, sujeto entre dos apoyos por los puntos A y B situados a la misma altura, forma una curva llamada catenaria. L distancia “ f” entre el punto mas bajo situado en el centro de la curva y la recta AB, que une los apoyos , recibe el nombre de flecha. Se llama vano a la distancia “a” entre los dos puntos de amarre A y B (figura N° 2.7).
Figura N° 2.7
Los postes deberán soportar las tensiones T A y T B que ejerce el conductor en los puntos de amarre. La tensión T = T A – T B dependerá de la longitud del vano, del peso del conductor, de la temperatura y de las condiciones atmosféricas.
Para vanos de hasta unos 500 metros podemos comparar la forma de la catenaria a la de una parábola, lo cual ahorra unos complejos cálculos matemáticos, obtenidos, sin embargo, una exactitud mas que suficiente.
Calculamos a continuación la relación que existe entre la flecha y la tensión. Para ellos representaremos el conductor de un vano centrado en unos ejes de coordenadas (figura N° 2.8):
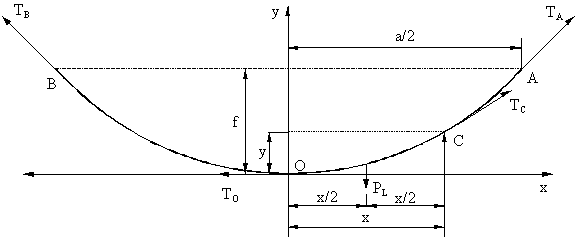
Figura N° 2.8
Consideramos un trozo de cable OC que tendrá un peso propio P L aplicado en el punto medio y estará sometido a las tensiones T O y T C aplicadas en sus extremos.
Tomando momentos respecto al punto C tendremos:
(2.1)
Por lo tanto el valor de y será:
(2.2)
Si llamamos P al peso unitario del conductor, el peso total del conductor en el tramo OC, que hemos llamado P L , será igual al peso unitario por la longitud del conductor, que cometiendo un pequeño error denominaremos x.
Por lo tanto admitiendo que:
(2.3)
y sustituyendo esta expresión en la fórmula anterior del valor de y resulta:
(2.4)
Si ahora consideramos el punto A correspondiente al amarre del cable en vez del punto C, tendremos que:
(2.5)
(2.6)
Por lo tanto al sustituir queda:
(2.7)
Podemos despejar el valor de la tensión T O y tendremos que :
(2.8)
La ecuación 2.7 nos relaciona la flecha f en función de la tensión T O , del peso unitario del conductor P y de la longitud del vano a.
Si comparamos esta ecuación de la parábola con la de la catenaria:
(2.9)
Podremos observar la complejidad de ésta, y como demostraremos más adelante, los resultados serán prácticamente iguales.
Nos interesa trabajar con la tensión T A en lugar de la empleada hasta ahora T O . Observamos el triángulo de fuerzas compuesto por T O , T A y P L (figura N° 2.9):
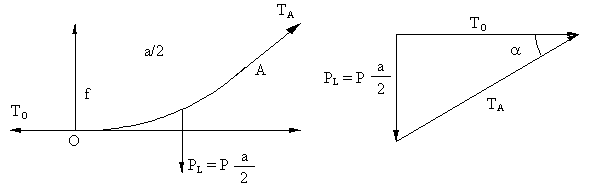
Figura N° 2.9
y aplicando el Teorema de Pitágoras tenemos:
(2.10)
En los casos prácticos que se nos presentan en las líneas aéreas de alta tensión, el valor del ángulo a formado por T O y T A es muy pequeño, por lo que podemos asegurar que T O @ T A , aproximación que emplearemos en cálculos posteriores. Esto equivale a afirmar que la tensión a lo largo del conductor es constante.
Referente a T A , podemos decir que esta tensión no debe sobrepasar nunca el valor de la carga de rotura del conductor Q , pues de lo contrario se rompería:
(2.11)
Siendo s el coeficiente de resistencia a la tracción del conductor utilizado y S la sección del mismo.
Puesto que un conductor no debe trabajar nunca en condiciones próximas a las de rotura, se deberá admitir un cierto coeficiente de seguridad n tal que:
(2.12)
2.9.2.1.- Comparación entre la catenaria y la parábola
Con un conductor HAWK calculamos las flechas para distintos vanos con un coeficiente de seguridad de 4. El conductor HAWK presenta una tensión de rotura de 8.820 kg y un peso unitario de 0,975 kg/m.
La flecha para la catenaria es:
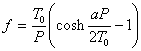(2.13)
La flecha para la parábola es:
(2.14)
Los valores que sustituimos son:
(2.15)
De esta forma elaboramos la tabla N° 2.4, en la que aparece la longitud del vano en metros, la flecha para la catenaria y para la parábola en metros y la diferencia entre los dos valores expresada en tanto por ciento.
Tabla N° 2.4
Vano |
Catenaria |
Parábola |
% |
100 |
0.553 |
0.553 |
0.005 |
200 |
2.213 |
2.213 |
0.017 |
400 |
8.857 |
8.852 |
0.065 |
600 |
19.945 |
19.916 |
0.146 |
800 |
35.499 |
35.406 |
0.261 |
1000 |
55.548 |
55.322 |
0.407 |
12000 |
80.133 |
79.664 |
0.585 |
1400 |
109.302 |
108.432 |
0.796 |
1600 |
143.111 |
141.624 |
1.038 |
1800 |
181.627 |
179.244 |
1.312 |
2000 |
224.925 |
221.289 |
1.616 |
Como podemos comprobar de la observación de la tabla, es suficiente aproximación el empleo de la parábola, sobre todo para vanos inferiores a 1000 metros.
2.9.3.- Longitud del Conductor.
Dada la flecha que se produce en un vano, la longitud del conductor no es igual a la distancia entre los postes. Por lo tanto, para hallar el valor exacto del conductor empleado, obtendremos la expresión de la longitud del conductor en un vano, en función de la flecha y de la distancia entre los postes (figura N° 2.10).
Figura N° 2.10
Tomamos un elemento diferencial de longitud dl, para el que se verifica:
(2.16)
Podemos multiplicar y dividir por dx 2 :
(2.17)
Del apartado anterior sabemos que (T = T O = T A ):
(2.18)
y derivando respecto a x podemos obtener el valor de dy/dx:
(2.19)
Por lo tanto al sustituir dx/dy en la expresión de dl 2 , nos queda:
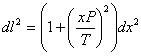(2.20)
Para no arrastrar expresiones llamamos a a:
(2.21)
y la expresión de dl resulta:
(2.22)
Para resolver el corchete empleamos la fórmula del binomio de Newton:
(2.23)
La longitud del conductor en la mitad del vano se obtiene integrando dl desde 0 hasta x:
(2.24)
Integrando cada sumando resulta:
(2.25)
Sustituyendo a por su valor 
queda:
(2.26)
Como x = a / 2 y la flecha es y = f queda:
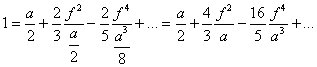(2.27)
La longitud del conductor en la totalidad del vano será el doble que en la mitad, por lo tanto L = 2 l, es decir:
(2.28)
Para vanos normales, sólo se emplean los dos primeros términos, pues la aproximación es más que suficiente:
(2.29)
Teniendo en cuenta la ecuación de la flecha:
(2.30)
La longitud total del conductor queda:
(2.31)
2.9.4.-
Acciones sobre los Conductores :
Para efectuar el cálculo mecánico de un conductor es fundamental conocer cuáles son las fuerzas que actúan sobre el mismo. En principio, se puede pensar que la única fuerza que actúa sobre el conductor es la fuerza de tensado, pero es necesario tener presente que ésta es la consecuencia equilibradora de las demás acciones, ya que, si el conductor estuviera en el suelo, la tensión para mantenerlo recto sería nula.
De esta forma se ve que es el peso de un conductor el que crea la tensión a la que está sometido. Así pues, el primer dato que debe considerarse es su propio peso, pero además existirán acciones importantes debidas a las inclemencias atmosféricas (hielo, frío, calor o viento).
Se divide la acción de la carga sobre los conductores en 3 partes (tabla N° 2.5):
Tabla N° 2.5
Tipo carga |
r (mm) |
p (gr/cm 2 ) |
t °c |
K |
Pesada |
12.7 |
1.95 |
-17.8 |
0.432 |
Mediana |
6.3 |
1.95 |
-9.5 |
0.283 |
Liviana |
0 |
4.4 |
-1.1 |
0.074 |
Donde:
r : Espesor radial de la capa de hielo (figura N° 2.11)
p : Presión del viento
t° : Temperatura
K : Constante (factor de seguridad)
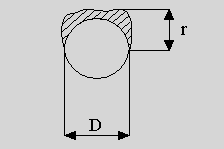
Figura N° 2.11
El viento actúa de forma horizontal, mientras que el peso del conductor lo hace verticalmente. Por locuaz debemos componer ambas fuerzas (figura N° 2.12)
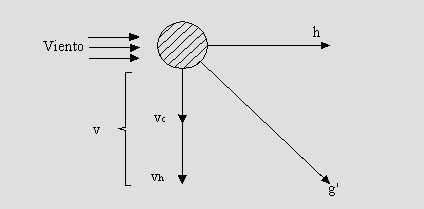
Figura N° 2.12
La resultante g' es la fuerza resultante en un conductor sometido a la acción del viento:
(2.32)
(2.33)
(2.34)
(2.35)
Donde:
g´ : Fuerza resultante (kg/m)
h : Componente horizontal producto de la presión del viento (kg/m)
v : Carga total vertical (kg/m)
v c : Peso propio del cable (kg/m)
v h : Peso correspondiente al hielo (kg/m)
D : Diámetro del conductor (mm)
r : Espesor radial de la capa de hielo (mm)
p : Presión del viento (gr/cm 2 )
D ebido a los cambios de temperatura, el conductor se dilata o se contrae. Esto origina variaciones en la tensión y en la flecha, que aunque no son muy importantes en vanos de pequeña longitud, deberemos tenerlas en cuenta en el cálculo mecánico.
El peso del conductor no dependerá de la temperatura, lo consideraremos constante, esto dependerá del viento y el hielo.
Como la dilatación es lineal responde a la ecuación:
(2.36)
Donde:
L 0 : Longitud del conductor a cero grados (m)
L 1 : Longitud a la temperatura t (m)
a : Coeficiente de dilatación lineal (°C -1 )
t : Temperatura considerada (°C)
Para hallar la variación de la longitud entre dos temperaturas diferentes t 1 y t 2 haremos:
(2.37)
Cuando un conductor está sometido a una determinada tensión, se produce un alargamiento de su longitud que responde a la ley de Hooke.
Llamando e al alargamiento elástico producido por un kilogramo, sobre un conductor de un metro de longitud y un milímetro cuadrado de sección, tendremos que en general, el alargamiento producido por una tensión T 1 o T 2 sobre un conductor de longitud L O y sección S será:
(2.38)
(2.39)
(2.40)
y siendo el llamado módulo de elasticidad 
, tendremos:
(2.41)
Ecuación que nos permite saber la variación de longitud del cable cuando esta sometido a una variación de tensión, T 1 , T 2.